Model #1 is the simplest of the models and contains three basic assumptions: (1) the springbok connecting the two masses obeys Hooke's law, (2) the mass of the spring is negligibly small, and (3) all dissipative effects can be ignored, including energy loss as the spring oscillates. Although these assumptions are not completely satisfied by a real springbok, the model describes the qualitative features of the springbok's motion quite well.

Model #2 attempts to improve upon Model 1 by taking into account the mass of the spring. Model #2 assumes that the spring is (to first approximation) uniformly stretched. This assumption leads to a solvable model that includes the mass of the spring. Two conditions must hold for this assumption to be realized in practice: (1) the spring mass must be small compared to the attached masses and (2) the spring must be stiff.

Model #3 attempts to improve upon Model 1 by taking into account damping effects. Model #3 assumes a damping force that is proportional to the relative velocity of the two springbok masses. This model does not attempt to take into account sliding friction.

Model 1

Free-body diagrams for the two masses and the springbok system are shown in the figure. Applying Newton's second law to each mass produces two coupled equations of motion. One way to solve the equations of motion is to divide the motion into two phases: phase 1 --- while the springbok is in contact with the base, and phase 2 --- after the springbok has left the table.

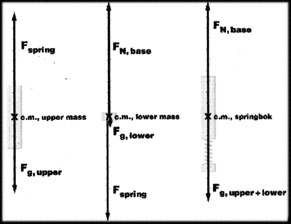
In the above equations, mu is the upper mass, ml is the lower mass, k is the spring constant, L is the natural length of the spring, g is the gravitational field strength and FN is the normal force exerted on the lower mass by the table.

The equations of motion for phase 2 have a simpler form and are easier to solve when written in terms of the total mass M, reduced mass (muml/M), center-of-mass coordinate (MY = muyu + mlyl), and relative coordinate (y = yu - yl).

The equations of motion and solution for phase 2 are as follows (sorry for the ghastly color scheme --- it looked okay when we typeset it many years ago, for a much earlier web site with a different color scheme):

The equations of motion and solution for phase 1 are as follows:

Model 2

In model 2 we assume that the spring has mass, but is always stretched uniformly. If a spring is stretched uniformly then it is straightforward to compute the kinetic energy and potential energy of the spring in terms of the upper and lower mass positions and velocities.

How the kinetic energy and potential energy impact the equations of motion is most easily seen by considering the Lagragian for the system.

Model 3

Model #3 assumes a damping force that is proportional to the relative velocity of the two springbok masses. This model does not attempt to take into account sliding friction. To obtain a "simple" expression for the time at which the springbok leaves the table, we assume that the damping coefficient is small.