Extracted from a booklet accompanying a workshop for high school science teachers.

by Robert J. Dufresne, William J. Leonard, and William J. Gerace

Our group at UMass [PERG] has developed a cognitive model that helps us to represent the differences in the ways that experts and novices store and use content knowledge. The Model also helps us to target specific areas on which novices need to concentrate in order to become better problem-solvers. However, the Model is only one representation of the structure of knowledge, and it is constantly evolving. Thus, it must not be taken too literally. Its usefulness comes from its ability to provide a concrete manifestation, however imperfect, of the ways in which experts and novices think. The Model helps us to discuss:

1. the storage of domain-specific knowledge;
2. expert- and novice-like problem-solving behavior;
3. the hierarchical structure of an expert's knowledge store;
4. misconceptions;
5. the effects of goal-free and goal-directed questions; and
6. the meta-communication process.

General structure of knowledge

In this workshop---and in our approach to physics in general---there are 3 basic themes:

1. Particular types of knowledge and knowledge structures are needed for proficient problem-solving. Much of this knowledge is conceptual in nature, as opposed to operational or procedural, and powerful knowledge structures necessarily involve conceptual elements. The presence of conceptual elements in the knowledge structures is the key to having a "deeper understanding" of physics.
2. Particular types of cognitive processes are required for the acquisition of conceptual knowledge and the construction of useful knowledge structures.
3. It is possible to design activities that promote these desirable cognitive processes. In many cases, these activities are simply actualizations of the cognitive processes themselves. (This point will, hopefully, become clearer later.)

We will elaborate on each of these themes before focusing on specific examples.

Theme 1: What do students need to know and how should what they know be structured for efficient problem-solving?

We begin by identifying some of the various types of knowledge that students need to know:

• Conceptual knowledge, such as the concept of momentum or energy, or that the velocity of an object changes when it accelerates, or that the gravitational potential energy of an object decreases as it falls.
• Factual knowledge, such as the value of the gravitational constant g, the radius of the moon, or the density of iron.
• Representational knowledge, such as how to draw and use graphs.
• Strategic knowledge, such as the ability to recognize the applicability of a concept, such as, momentum is conserved when there are no external forces, or that energy is conserved when there are no non-conservative forces.
• Meta-cognitive knowledge, for example, the awareness of underlying assumptions, or that an answer should be checked by solving the problem a different way.
• Self knowledge, such as knowing one's likely sources of mistakes, or knowing that one should be more procedural when solving problems.
• Operational knowledge, such as how to take the cross product or dot product of two vectors, or how to take the determinant of a matrix, or how to draw a free-body diagram.
• Procedural knowledge, such as when to use conservation of energy (i.e., when all forces are conservative), or when to specify a coordinate system (e.g., when finding potential energy), or when to draw a free-body diagram (e.g., when applying Newton's Laws).
• Problem-state knowledge, which are the features of a problem used for deciding how to solve it. Examples are: knowing that there are no external forces in a particular problem, or that there are no non-conservative forces in the problem, or that an object is at rest initially, or that the object is on an incline.

These types of knowledge need to be organized and structured for efficient use when problem-solving. In order to discuss the organizational and structural aspects of knowledge, we have found it convenient to broadly classify these types into three general categories. We call these three groups: Conceptual Knowledge, Operational and Procedural Knowledge, and Problem-State Knowledge. In Fig. 1, these three general categories are shown in a representation of how experts store content knowledge.

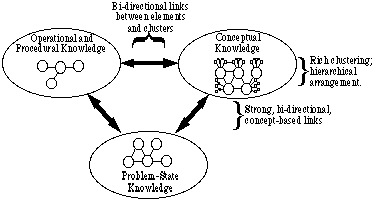Fig. 1: A representation of an expert's structure of knowledge

The expert has a rich clustering of concepts, in which each concept is related to many other concepts, and the relationships between concepts are clearly understood. Concepts are arranged hierarchically using umbrella concepts to more tightly relate them. In fact, umbrella concepts are used to group elements within each of the three categories. The expert has a large store of problem-state knowledge, including much information about which principles apply to particular situations. The expert also has a large store of equations, operations, and procedures (EOPs) that can be quickly accessed.

The links between each pair of categories are very strong: Problem states are strongly linked to concepts and to EOPs, which are themselves strongly linked to each other. The same umbrella concepts are used to group concepts, problem states, and EOPs. Therefore, for any particular problem, concepts can be used to decide the appropriateness and applicability of equations, and the utility of specific operations and procedures.

(One must be very careful here not to be too rigid in one's thinking, because it is easy to disagree about which of these categories should be used to classify a particular element of knowledge, or whether it belongs in only one category. Our purpose is simply to have a mechanism for visualizing the several levels of association that can occur between elements.)

We tend to use the term linking to mean a formed association between two elements of the same or different knowledge types, and the term clustering to refer to associations between several elements or clusters. What makes this kind of discussion very difficult is that there is a kind of iterative process going on here: A very strong bond between three items---a conceptual cluster, the recognition of the circumstances making the concept applicable, and the procedures needed to apply the concept---forms a new type of knowledge element which we put into Strategic Knowledge (a fourth category). This new knowledge element is what some refer to as a schema and often involves problem-state knowledge as well. Since the knowledge element is conceptual in nature, it becomes replicated (i.e., repeated) in the conceptual bubble.

If we take a closer look at the conceptual bubble, we see some of the specific types of conceptual knowledge, for example, Representational Knowledge, Strategic Knowledge, Meta-Cognitive Knowledge, and Knowledge of Basic Concepts. This is represented in Fig. 2. (Other types of conceptual knowledge are not shown.)

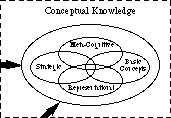Fig. 2: Types of conceptual knowledge

How is a novice's structure of knowledge different from an expert's? As represented in Fig. 3, novices generally have a poor clustering of concepts. Many links are inappropriate; others are non-existent. Some of the inappropriate links are extremely strong, which leads to misconceptions. Novices generally do not use umbrella concepts to group elements. They have a small store of problem situations, in which surface features are used to cluster them together and to decide how problems should be solved. They are familiar with a relatively large number of equations, but they often remember them incorrectly or need to look them up in order to use them. They have been taught operations and procedures, but they are not yet proficient at them. Therefore, it cannot be said that they "know" them.

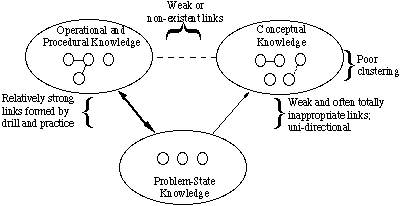Fig. 3: A representation of the novice's structure of knowledge

Links between concepts and EOPs are weak or non-existent. Links between concepts and problem situations are also weak. Thus, a novice cannot analyze a problem and cannot decide the appropriateness of particular equations. The links between problem situations and EOPs are relatively strong, but the links are based primarily on the quantities that the equations have in common with the givens and explicit unknowns of the problem.

Theme 2: In what kinds of cognitive processes must students engage to develop appropriate knowledge structures?

To answer this question, we must first understand how experts and novices solve problems differently.

Novices are generally unsuccessful when they try to solve typical problems in physics. Using the Model to represent the process, how does a typical novice solve a problem? Because the strongest links in the novice's structure of knowledge are between problem situations and equations, reading a problem immediately suggests equations involving the quantities (known and unknown) explicitly given in the problem. Without determining the applicability of those equations, and without trying to think of other equations that might involve the same quantities, the novice usually starts to manipulate the most familiar equations until the unknown can be solved for. The most recent equation covered in class is the most easily accessible and the most quickly recalled. Thus, the novice looks for and (if "successful") finds only one way to solve a problem and usually stops, without investigating other possibilities and without analyzing the problem situation. The equations found this way are often inappropriate because novices often don't use concepts to justify their application. Even if students are driven to invoke concepts by analyzing problems beforehand, their links to EOPs are generally too weak to be useful for problem-solving. Also, links between concepts and problem situations are uni-directional, so analogies are not particularly useful: Novices can't use analogies to solve problems because they can't identify which of the problems they have already solved are conceptually similar to the one they are currently trying to solve. Instead, novices use surface features to establish "similarity" and try to solve new problems based on their similarity to the surface features of problems they've already solved.

Because experts classify problems and EOPs according to the same umbrella concepts, they can often go directly from problem situations to appropriate equations, operations, and/or procedures. Because the links between different categories are strong, difficult problems (ones for which a direct link between problem states and EOPs does not yet exist) can be solved by consciously invoking concepts, thereby indirectly connecting problem states to the appropriate EOP(s). Because the links between concepts and problem situations are bi-directional, analogies are an extremely useful problem-solving tool for experts. Finally, experts usually have more than one approach to solving any particular problem.

Here is a summary of the major differences between experts and novices:

1. Novices have a poor clustering of concepts, which often leads to misconceptions. Experts have a rich clustering of concepts, problem situations, equations, procedures, and operations, which leads to improved problem-solving ability.
2. Novices usually have only one way of solving a particular problem, whereas experts often can find more than one way. Therefore, the expert can attempt to resolve inconsistencies when they occur and check answers, while novices are unaware that inconsistencies exist and cannot check their answers.
3. Novices often use equation manipulation and seldom use concept-based strategies to get an answer. The expert uses concepts and analogies to suggest several methods of solution and plans a strategy for finding the correct answer.
4. Novices often fail to get the right answer, and when they do get the right answer it can easily be for the wrong reason. When the novice gets the right answer for the wrong reason, misconceptions are reinforced and become even harder to overcome. An expert usually gets the right answer and can explain why the answer is correct.

There are a variety of cognitive processes beneficial for helping novices develop a concept-based problem-solving approach, which we divide into three categories: Analysis Processes, Reasoning Processes, and Meta-Cognitive Processes.

Analysis processes

• Problem analysis, such as constructing a problem representation.
• Conceptual analysis, such as using concepts to determine the qualitative behavior of physical objects or to form a strategy.
• Strategic analysis, such as identifying and justifying physics principles relevant to a problem situation.
• Representational analysis, such as exploring different representations of a problem.
• Complex constructive analysis, such as decomposing a complex situation into simpler ones.

Reasoning processes

• Comparing and contrasting, such as identifying how items, situations, or conditions are similar and/or different.
• Interpreting, for example, using the shape of a plot of position vs. time to estimate the acceleration of the object.
• Special and limiting cases, that is, exploring extreme and/or known conditions.
• Prototype and counter-examples, for example, generating archetypical categories.
• Generalization, that is, recognizing the salient features of a circumstance or situation.

Meta-cognitive processes

• Reflection, that is, self-directed review of purpose, goals, effects of experience, etc.
• Meta-communication, which is conscious participation in establishing and refining lines of communication with the teacher and other students, and in deciding the goals of learning.
• Self-evaluation, such as evaluating one's performance, or identifying reasons that difficulties were encountered while solving a problem.

These and other processes are encouraged by our curriculum materials. The specific types of activities to do this are presented in the next section.

Theme 3: What types of learning activities or experiences promote these beneficial cognitive processes?

The following activities can be used by teachers to stimulate the cognitive processes needed to develop a conceptual understanding of physics:

1. Use multiple representations. A representation may be linguistic, abstract, symbolic, pictorial, or concrete. Using many different representations for the same knowledge, and having students translate between representations, helps the student to inter-relate knowledge types and relate the knowledge to physical experience. It encourages the formation of links between knowledge elements and promotes a rich clustering of knowledge.
2. Make forward and backward references. Concepts require a long time to be formed. Thus, you cannot wait for students to completely learn one topic before moving on to the next. By making forward references, you prepare the student for new material. By making backward references, you associate new material with established (or partially established) material, thus making knowledge interwoven and interconnected, rather than linear.
3. Explore extended contexts. Concepts can be extremely context dependent and do not become globally useful until they are abstracted. Investigating a broad context of applicability helps the student to refine and abstract concepts. It also avoids incorrect or oversimplified generalizations.
4. Compare and contrast. Essential to the process of structuring (or re-structuring) knowledge is the classification and inter-relation of knowledge elements. Comparisons and contrasts sensitize students to categories and relationships, and helps students perceive the commonalities and distinctions needed to organize their knowledge store.
5. Categorize and classify. In parallel with comparisons and contrasts, students must be aware of categories and classification systems. Students must also practice creating and recognizing categorization systems. By requiring students to classify items, to choose names for their categories, and to explain their system, we can help students re-structure their knowledge store.
6. Predict & Show (inadequacy of old model). Carefully selected demonstrations and experiments can be used to bring out inconsistencies in student models. Students should be shown a set-up or experimental apparatus and should be asked to predict what will happen when something is done. It is important that students make predictions beforehand, thus making them aware of their own model. Students will consider alternate conceptions only if their own fails. Requiring students to use their models and showing them how their models are inconsistent or inadequate will prepare them to create better (though still their own) models.

7. Explain (summarize, describe, discuss, define, etc.). Standard problems seldom tell the teacher what students don't understand. Even when students get a problem right, there can still be confusion about the applicability of the equations used. Requiring students to explain how they will solve a problem exposes misunderstandings and misconceptions, and helps students reorganize their knowledge store. In addition, students seldom see in standard demonstrations and experiments what experts see. Students should explain and discuss what they think they've seen (during Predict & Show, for example), so that the teacher can interact with the students' models. Furthermore, the process of explaining (or summarizing, describing, discussing, etc.) helps students become aware of their own models as well as the models of other students.

8. Generate multiple solutions. Efficient problem-solving cannot occur unless students choose from a set of valid solution paths. By solving problems in more than one way, students learn to prioritize elements of their Strategic Knowledge.

9. Plan, justify, and strategize. Very few relationships in physics are always valid. To avoid equation manipulation, students should be asked to plan (and then explain) how they will solve problems. Students must learn how to determine which concepts are relevant (and which are irrelevant) for any particular problem situation and how to implement the relevant concepts to solve that problem. Having students generate their own strategies helps them to learn how concepts are used to solve problems.
10. Reflect (evaluate, integrate, extend, generalize, etc.) After completing most activities, students benefit from looking back on what they've done. What patterns have they perceived? What general rules can be constructed? Other types of activities give students the pieces needed to create a coherent picture of physics, but some sort of reflective activity is usually needed to "put the pieces together".
11. Meta-communicate about the learning process. To learn physics (or any other complex subject), students must become self-invested. They must be exposed to other people's (teacher's and student's) models. They must be warned that precision in communication is essential; they must be informed of common pitfalls and misinterpretations; and they must be told that they should re-structure their knowledge. Students must learn how they learn best.