Springbok
(This is a companion website to the article Springbok: The physics of jumping, published in The Physics Teacher.)
Springbok is our name for a simple mechanical system for teaching about the physics of jumping. A springbok consists of a large mass and a small mass connected by a spring; when compressed and then released, it jumps up into the air.
(The name "springbok" comes from a South African gazelle noted for its grace and its delightful habit of springing suddenly into the air.)
A springbok is easy to make and engaging to study. It provides a rich context for exploring a wide range of physics concepts and principles, and it possesses a number of features that give it broad instructional value. There is much a student can learn about the physics of jumping from a purely conceptual analysis of this toy.
However, the simplicity of the spring-loaded design also allows for a straightforward quantitative analysis of jumping. A springbok is ideal for hands-on projects and science competitions. With an appropriate focus, a springbok can be used in a variety of instructional settings, from high school physical science to graduate mechanics.
An article providing both a conceptual and quantitative analysis of the springbok (the mechanical system, not the gazelle) can be found in the published paper Springbok: The physics of jumping.
Modeling a Springbok
Model #1 is the simplest of the models and contains three basic assumptions: (1) the springbok connecting the two masses obeys Hooke's law, (2) the mass of the spring is negligibly small, and (3) all dissipative effects can be ignored, including energy loss as the spring oscillates. Although these assumptions are not completely satisfied by a real springbok, the model describes the qualitative features of the springbok's motion quite well.
Model #2 attempts to improve upon Model 1 by taking into account the mass of the spring. Model #2 assumes that the spring is (to first approximation) uniformly stretched. This assumption leads to a solvable model that includes the mass of the spring. Two conditions must hold for this assumption to be realized in practice: (1) the spring mass must be small compared to the attached masses and (2) the spring must be stiff.
Model #3 attempts to improve upon Model 1 by taking into account damping effects. Model #3 assumes a damping force that is proportional to the relative velocity of the two springbok masses. This model does not attempt to take into account sliding friction.
Model 1
Free-body diagrams for the two masses and the springbok system are shown in the figure. Applying Newton's second law to each mass produces two coupled equations of motion. One way to solve the equations of motion is to divide the motion into two phases: phase 1 --- while the springbok is in contact with the base, and phase 2 --- after the springbok has left the table.
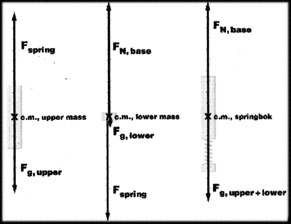
In the above equations, mu is the upper mass, ml is the lower mass, k is the spring constant, L is the natural length of the spring, g is the gravitational field strength and FN is the normal force exerted on the lower mass by the table.
The equations of motion for phase 2 have a simpler form and are easier to solve when written in terms of the total mass M, reduced mass (muml/M), center-of-mass coordinate (MY = muyu + mlyl), and relative coordinate (y = yu - yl).
The equations of motion and solution for phase 2 are as follows (sorry for the ghastly color scheme --- it looked okay when we typeset it many years ago, for a much earlier web site with a different color scheme):

The equations of motion and solution for phase 1 are as follows:

Model 2
In model 2 we assume that the spring has mass, but is always stretched uniformly. If a spring is stretched uniformly then it is straightforward to compute the kinetic energy and potential energy of the spring in terms of the upper and lower mass positions and velocities.
How the kinetic energy and potential energy impact the equations of motion is most easily seen by considering the Lagragian for the system.


Model 3
Model #3 assumes a damping force that is proportional to the relative velocity of the two springbok masses. This model does not attempt to take into account sliding friction. To obtain a "simple" expression for the time at which the springbok leaves the table, we assume that the damping coefficient is small.


Questions to Ponder
Before proceeding to the rest of the web site, we suggest you try answering some basic questions about a springbok.
- Why does a springbok jump?
- What forces do work on a springbok?
- What is the source of energy for a jumping springbok?
- What forces provide an impulse to the springbok?
- Under what circumstances will it leave the table --- e.g., will it leave the table if the masses on the two ends are equal?
- What factor(s) determine how high a springbok will jump --- e.g., will it reach the same height on the moon as on the earth?
- If the masses on the two ends are unequal, for which orientation of the masses will the springbok jump the highest?
Building a Springbok
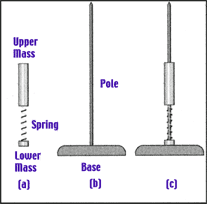 To make a springbok, simply attach two masses to opposite ends of a spring [Figure 1]. A guide-pole and base are needed to maintain stable vertical motion [Figure 2]. The masses we used in our 'boks are made of aluminum, as are the guide poles. Other materials can be used; just keep in mind that it is best to reduce the friction force between the two masses and the pole as much as possible.
To make a springbok, simply attach two masses to opposite ends of a spring [Figure 1]. A guide-pole and base are needed to maintain stable vertical motion [Figure 2]. The masses we used in our 'boks are made of aluminum, as are the guide poles. Other materials can be used; just keep in mind that it is best to reduce the friction force between the two masses and the pole as much as possible.
To insure that the masses stay attached to the spring, machine a set of threads on each mass so that the spring can be "screwed" into place. Drill a hole through the center of the two masses so that they can slide along the pole.

Specifications
A 'bok can be made in different sizes:

When used as a demonstration, make sure that the 'bok jumps to a satisfactory height when the larger mass is on top. One can estimate how high a 'bok will jump (assuming it is made with a light, stiff spring) by using the following relationship:
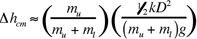
Be sure to select the ratio of the two masses so that the difference in the "jump height" for the two orientations of your 'bok (i.e., larger mass on top versus smaller mass on top) will be obvious. For a sufficiently stiff spring, the jump height is proportional to the upper mass, so the ratio of the jump heights is equal to the ratio of the two masses. We have used mass ratios as high as 9 to 1.
There are two other design issues to keep in mind when building a 'bok:
- Once a spring is selected, the only way to increase the jump height of the Springbok is to decrease its total mass. However, if you decrease the two masses too much, the spring mass will be comparable to one or both of the masses. If this is the case, a simple Hooke's Law model that ignores the mass of the spring will not provide an accurate description of your springbok system. To avoid this problem, start the building process by selecting a stiff lightweight spring. Then choose masses accordingly.
- The only other significant design issue is damping in the spring. Good agreement with a simple Hooke's Law model requires a spring with a small damping coefficient. Using a model that accounts for damping may be necessary to achieve good agreement between model predictions and data.
The two springboks used in the "QuickTime Clips" have the following specifications:
| large 'bok | tiny 'bok | ||
| masses (g) | |||
| small mass | 93.8 | 60.5 | |
| large mass | 240. | 275. | |
| spring | 59.0 | 70.0 | |
| elastic constants (N/m) | |||
| average value | 359. | 458. | |
| uncertainty | 15. | 13. | |
Damping coefficients for the two springs can be determined from "Quicktime Clips" of the masses oscillating while the 'bok is held fixed to a tabletop.
Cleaning and Lubricating
Sliding friction will decrease the performance of a 'bok, so you may wish to take steps to reduce it. Beyond making all contact surfaces as smooth as possible, you should clean and lubricate them. For our 'bok, which was made out of aluminum, we used a lacquer thinner to clean surfaces and graphite to lubricate them. We have also used silicone spray to both clean and lubricate.
Springbok Movies
Welcome to our collection of Springbok video clips. Click on a link below to view a Quicktime video. After viewing, click your browser's "back" button to return here.
Large Springbok Jumping:
- small mass up, large mass down
- large mass up, small mass down
- medium mass up, large mass down
- large mass up, medium mass down
Tiny Springbok Jumping:
Mass Oscillations: