Minds*On Physics

A constructivist, active-learning curriculum for high school physics
Contact(s): 
Leonard, William J.

MOP is a one-year curriculum for high school physics. It is the result of a materials development project supported by the National Science Foundation, and its design was guided by educational research findings. The curriculum integrates topics traditionally taught at different times of the year, and students are expected to develop conceptual understanding of physics while improving problem-solving proficiency.

What is MOP?

A description of the intent and nature of the Minds-On Physics curriculum

During the past two decades, study after study has pointed out the shortcomings of high school physics courses: (a) The vast majority of students who take high school physics emerge with only a shallow understanding of miscellaneous facts and formulas; (b) What knowledge students do acquire is usually plagued with misconceptions, many of which persist despite instruction; and (c) With rare exception, students are unable to apply what they learn to explain, or to reason about, the world around them or to solve interesting, nontrivial problems. These unintended outcomes of physics instruction are the result of a mismatch between the way physics is typically taught and the way students go about the business of learning physics.

The Minds•On Physics (MOP) curriculum materials were specifically written to address this situation. In developing MOP, we have endeavored to take account of research on the teaching and learning of physics, which has grown steadily during the past twenty years. This research has brought to light many of the cognitive difficulties students face in trying to learn physics (see Supplement B in the Teacher's Guide to accompany MOP: Motion). It has also demonstrated the value of an active learning environment and cooperative group work for improving student learning and maintaining student interest (see Supplements A and B in the Motion Teacher's Guide). MOP is designed to be consonant with findings from many different strands of educational and cognitive research - prior conceptions, expert vs. novice differences, the cognitive load associated with different styles of questions, problem solving vs. conceptual understanding, active learning, cooperative group learning, and the effects of meta-communication on the learning process. We believe that MOP will provide teachers with an approach to physics instruction that is better matched to the learning needs of students, and thereby improve the quality of the educational experience for both students and teachers.

MOP is an activity-based, full-year curriculum for high school physics. It is intended to be an excellent preparation for college-level science, and is well matched with the National Research Council's National Science Education Standards. (See Supplement C in the Motion Teacher's Guide for a comparison with the 1996 standards.) The MOP activities were designed to help students learn to use physics concepts to analyze and solve problems, and to curb students' natural tendency to learn by rote and to engage in formula manipulation. Most of the activities are well suited for use in cooperative group settings. Through careful construction and sequencing, MOP activities encourage students (a) to explore their existing understanding of physics-like concepts, (b) to refine their understanding of formal physics concepts and to investigate connections among related concepts, (c) to use physics concepts and principles to analyze and reason about physical situations without recourse to equation pushing, (d) to develop problem-solving skills that are anchored in an understanding of fundamental concepts and principles, and (e) to put together seemingly isolated pieces of physics knowledge into a unified, meaningful whole. Our goal is to enable students to obtain a deeper understanding of physics concepts and a greater facility for applying them to novel situations - or at the very least to point them in the right direction.

Although the MOP activities place a premium on conceptual development, the MOP curriculum should not be viewed as a traditional conceptual-physics curriculum. Many MOP activities require a fairly high level of analytical reasoning and mathematical skill, more comparable to traditional problem-solving physics courses than to conceptual-physics courses. Similarly, MOP engages students in conceptual reasoning at a much deeper level than is typically the case in a conceptual-physics course - for that matter in any type of high school physics course. MOP is a challenging and rigorous course!

Nevertheless MOP is flexible enough to be used with a wide range of students. For example, MOP activities have been used in 8th and 9th grade physical science courses, and they have been used in graduate-level teacher preparation courses. This is possible because of the way MOP activities are sequenced. Initial activities focus on the students' understanding of concepts. Later activities help students build and refine a scientific understanding of physics concepts. Only then are students asked to do the more challenging activities that require complex analysis and reasoning skills. The quantitative/mathematical development of a topic only occurs after students have had sufficient opportunity to develop a thorough conceptual understanding. We believe that MOP can provide all students with the skills needed to succeed in physics, and that the materials help create a classroom environment that is active and inclusive.

Another reason many different levels and types of classes can use MOP is that the depth of coverage is determined by the teacher and the students, not the activity. This is the beauty of having questions at the core of the curriculum. Students at different stages of development will necessarily interpret them differently, and their answers will always reveal the depth and breadth of their understanding. And teachers can probe as much or as little as they desire into their students' thought processes.

Activities are the heart and soul of the MOP curriculum materials, but the MOP program is more than a set of student activities and associated materials. It is an approach to learning physics. Underlying the approach is a set of four basic principles:

In recognition of these principles, MOP advocates an action-oriented approach to learning physics. This means that MOP encourages little (if any) lecturing by the teacher, and requires minimal reading by the student prior to working on an activity. Instead, after a brief introduction to a new topic, students are quickly engaged in activities that require them to interact with other students and the teacher. Working in groups students use concepts to analyze problem situations and answer open-ended questions, explore the meaning of concepts through inquiry and hands-on activities, and share personal reflections on prior experiences. The approach treats students as sentient individuals, each one having a unique way of looking at a situation or solving a problem. The MOP approach builds on what students know, and it emphasizes processes, such as analyzing, reasoning, explaining and strategizing, over coverage of "physics facts."

Content of MOP. The MOP materials are contained in six volumes of student activities and six corresponding Teacher's Guides. The first three volumes of activities are the core of the MOP curriculum and can be covered in 1/2 to 3/4 of the school year. The first volume contains activities covering Motion. The second volume is on Interactions. The third treats Conservation Laws & Concept-Based Problem Solving. Taken together, we refer to these three volumes as mechanics.

The remaining three volumes constitute supplemental activities, which can be done for the final 1/4 to 1/2 of the school year. They are Fundamental Forces & Fields, Complex Systems, and Advanced Topics in Mechanics. The goal of each is to show how the concepts in mechanics can be applied to many other topics.

The materials require very little specialized or sophisticated equipment. In mechanics, most of the manipulatives that might be needed are common household items, such as balls, string, washers, marbles, and bathroom scales. However, it is helpful if teachers have access to basic equipment, such as dynamics carts, air tracks, and spring scales. Within the supplemental activities, some of the equipment needed is a little more specialized, but it should still be simple and familiar, such as batteries, magnets, wire, and nails.

Assessment. Traditional ways of testing students do little to uncover conceptual difficulties or to measure understanding of physical laws and principles. New ways of assessing students' progress must necessarily be developed alongside new approaches to teaching physics. New assessments need to encourage students to focus on those features that are important for deep understanding. In the Instructional Aids for Teachers, we provide a wealth of examples showing how to probe students' conceptual understanding and measure their progress with the new approach.

Role of Teachers. The MOP approach requires a different role for teachers. No longer are teachers dispensers of information. A teacher who uses the MOP approach spends less time preparing lectures and more time structuring experiences for students. Many activity questions actually have two or more justifiable answers, each of which depends on the assumptions made by the students answering the questions. Thus, emphasis should be shifted from answers and whether they are right or wrong, and placed on intelligent discussion of the questions and whether the answers are consistent with the assumptions and reasoning used. In this mode, a teacher serves as a facilitator, counselor, or coach, rather than a lecturer, turning students' attention toward those ideas that will eventually help them reach a satisfactory conclusion.

Materials and Support for Teachers. We have worked with teachers for many years. We are well aware of the difficulties teachers face in adopting a new curriculum, particularly if it is radically different from what they have used in the past. Realistically, it could take a teacher two to three years to become completely familiar with the MOP curriculum, and to make it their own. We have included with the MOP curriculum considerable support materials to make the transition easier and more manageable for teachers.

We hope that MOP will enrich your physics teaching and will help your students not only to learn more physics and to learn it better, but also to improve their thinking and learning skills. If we had to pick one word to emphasize, it would be communication. Two-way communication between the teacher and students is critical to the success of the educational endeavor. No set of fixed materials can ever be the total solution to an educational problem. Only teachers can act flexibly enough to meet all the needs of their students, and only through open dialogue between teachers and students can teachers determine fully the needs of their students, and students receive the feedback they need to remain constructively engaged in the learning process.

Development of the Minds•On Physics curriculum materials was supported by the National Science Foundation (NSF), under grants MDR-9050213 and ESI-9255713.

MOP vs. Standards

Does Minds*On Physics answer the call of the National Science Education Standards
When the standards say... Minds•On Physics replies...
Science is for all students. Everyone can learn physics. The MOP program presents physics as an exercise in analyzing and solving problems.
Learning is an active process. Since students learn in different ways, MOP offers a wide variety of activities so that every student experiences success.
Teachers should focus and support inquiries while interacting with students. MOP minimizes lecturing and maximizes student-student / student-teacher interaction.
Teachers should orchestrate discourse among students about scientific ideas. MOP activities and discussion are student-driven; students are active participants in their own learning.
Achievement data collected should focus on the science content that is most important for students to learn. MOP advocates a departure from the static, such as memorizing facts, to the dynamic, such as reasoning skill development.
Equal attention must be given to the assessment of opportunity to learn and to the assessment of student achievement. MOP activities are a continuous formative assessment of student thinking.
Assessment tasks should be authentic. MOP mimics professional science.
All students should develop abilities necessary to do scientific inquiry. MOP activities promote individual skills needed to do science, including both operational and critical thinking skills.

We developed Minds•On Physics with curriculum reform in mind. The program builds upon and expands students' knowledge about the physical world, getting students to think about and do science in a way that is meaningful to them.

AttachmentSize
MOP vs. Standards, Long Version (PDF)60.07 KB

Frequently-Asked Questions

Questons and answers about the Minds*On Physics curriculum

These questions are loosely based on ones asked by the Chicago Public Schools Board when they were considering adopting the MOP curriculum.

How does your program or materials line up with the Illinois Learning Standards or the NRC's National Science Education Standards?

See our comparison of the Minds•On Physics approach with the NSES (1996). A more detailed comparison can be found in the PDF attachment at the bottom of that page.

Do you have any data about student achievement in districts that have been using the program for a minimum of two years?

No, but the evaluation team headed by Allan Feldman said the following in their executive summary based on the beta field-testing:

When the MOP approach is used with the MOP materials as a comprehensive curriculum... students gain access to knowledge and skills that allow them to develop expert-like, concept-based problem solving abilities that are inaccessible with traditional curricula. In addition, students who used MOP regularly showed a greater awareness of their metacognitive process in solving physics problems than did students who used MOP only occasionally. (Feldman & Kropf, MOP Executive Summary, p.2, 7/23/97)

Can you give us some relevant background about the instructional framework of the materials and the research that guided the materials development?

The instructional framework for MOP is called Concept-based Problem Solving. The approach emphasizes analysis and reasoning over both pure conceptual understanding and pure numerical problem solving. Students spend a lot less time solving problems, but they develop deeper understanding and more robust problem-solving skills.

The developers are researchers in physics education, with credentials in expert-novice studies, metacognition, and bilingual research. The materials were developed using a cognitive framework based on multiple strands of educational research, including misconceptions, schema acquisition, cognitive overload, and the knowledge store and problem-solving techniques of experts and novices.

The approach is described in several sources. For instance, Supplement B of the (MOP) Motion Teacher's Guide is entitled Concept-based Problem Solving: Combining educational research results and practical experience to create a framework for learning physics and to derive effective classroom practices. A slightly shorter version can be found under the title Analysis-based Problem Solving: Making analysis and reasoning the focus of physics instruction.

Can you give us a detailed description of the development process, including the names of the primary developers and the pilot/field testing process, and a list of field or pilot test sites?

The development process can be divided into three phases: piloting, field-testing, and publishing. We started in 1990 with a team of four physics education researchers (UMPERG) and four high school teachers from a range of settings and with a range of skills and experience. The teachers reviewed the module activities drafted by UMPERG, making comments, corrections, and suggestions that were then used to revise the modules before piloting them. The teachers piloted the modules, gave UMPERG more advice about the materials, and allowed UMPERG into their classrooms to see how they were used and to talk to students. At the end of the pilot project in 1992, we had developed and tested 24 modules, covering only about 1/3 of the school year. The accompanying teacher support materials consisted of answers with short explanations to all of the module questions. The modules were developed under the National Science Foundation grant MDR-9050213.

In the field-testing phase (1993-97), we divided the modules into smaller activities that could be started and completed during the same class period. We also began developing additional activities in order to span a full year, and we added a "Student Reader" to summarize the ideas raised in the activities. The teacher support materials became "Answers and Instructional Aids for Teachers" with tidbits such as Preparation for Students, Anticipated Difficulties for Students, and Suggested Points for Class Discussion. We added 30 more teachers in Massachusetts, Tennessee, and Louisiana to field-test the materials, having meetings with local teachers every 6 weeks or so to gather insights and share experiences. Meetings with teachers in Chattanooga, TN and New Orleans, LA occurred less frequently but were just as informative. At the end of this phase, we had field-tested more than 100 activities. These activities were developed under NSF grant ESI-9255713.

In the publishing phase (1997-2003), we organized the activities into a "core" curriculum and a "supplemental" curriculum having three volumes each. The field-tested activities became the core curriculum, and we developed another 80 activities for the supplemental curriculum. We also organized and expanded the existing Answers and Instructional Aids for Teachers into more complete Teacher's Guides, one to accompany each volume of activities, and wrote Teacher's Guides for the three volumes of new activities. The last Teacher's Guide was published earlier this year.

For more detailed information about the actual development process, please refer to our model-based design paradigm as described in section IV of the technical report ASK-IT/A2L: Assessing Student Knowledge with Instructional Technology.

UMPERG [as of the writing of MOP --- ed] is William Gerace, Jose Mestre, Robert Dufresne, and William Leonard. All four are Physics PhDs with extensive teaching and research experience. They have conducted more than 60 workshops and mini-courses on learning and instruction, have written numerous articles on educational issues, given almost 200 talks on physics instruction, and done more than 70 science demonstration shows for nearly 2000 school children in the U.S. and South Africa. (These shows demonstrate how physics is manifest in everyday situations with common items.)

The pilot sites were in four very different settings. One is an excellent private school in NW Massachusetts. Another is a suburban HS with a diverse student population. A third is an average urban HS in Springfield, MA, with a large, though not predominantly, minority student population, and the fourth is an inner city, bottom-rung, 100% minority, school-of-last-resort for students in Hartford, CT.

The pilot teachers are also very different. One has an Ed.D. from the University of Massachusetts, and has even co-authored his own instructional manual for teachers. He is involved in lots of innovative programs, and is always willing to try something new. The second is a traditional teacher, well trained in physics and not overly creative in his teaching. The third is a biology teacher with almost no content knowledge teaching physics, but he is brilliant in creating group activities, however, and we learned much from him about adapting our materials to group work. The fourth is an energetic and highly adaptable physics and astronomy teacher.

A list of the field-test teachers can be found in the Acknowledgments of any one of the Student Activities books. There are 34 in all. Most are located in Massachusetts, but one cadre was located in and around Chattanooga, TN, and another was located in and around New Orleans, LA.

How does the program or materials address diversity in the student population?

Diversity is not limited to ethnic and cultural diversity. Every student has a unique set of skills, past experiences, and approaches, and so, in Minds•On Physics, we show teachers that there are many paths to success and many different ways to do physics. If a student, for example, does not have the algebraic skills to solve a traditional problem, we show how to help that student reason through to an answer. If a school system does not have a large equipment budget, we show them how to think and live and do physics without any expensive equipment.

If you look at MOP, you will see an emphasis on thinking, analyzing, and reasoning, which anyone can be encouraged to do at any age with almost any background. Also, you will see common everyday manipulatives, such as balls, toy cars, and rubber bands, items that students are familiar with and almost any school system can afford.

MOP is activity-based, which means the teacher decides the depth and level of coverage. MOP has been used in many different contexts, such as 8th and 9th grade physical science, 11th and 12th grade college prep physics, as supplementary materials in introductory college physics, and in graduate level teacher preparation courses. There are even a few students I know who have used the "Complex Systems" volume to help them with their Junior level (University) Statistical Physics class.

MOP has been used in schools with large minority student populations in Chattanooga, TN, New Orleans, LA, Springfield, MA, and Hartford, CT, and MOP has recently been adopted by Grand Rapids, MI. MOP has also been used in "bridging" programs for under-prepared black university students in South Africa.

Have you done an external evaluation of the materials by objective and respected sources?

The evaluation of Minds•On Physics was done by a team of researchers led by Allan Feldman of the University of Massachusetts School of Education. An executive summary is available.

AttachmentSize
MOP Evaluation Executive Summary41.25 KB

MOP Contents

Tables of contents for the books of the MOP series

The MOP curriculum consist of four reusable Activities & Reader books for students (paperback, 8.5" x 11"), which together span a complete full year curriculum for high-school physics.

For each of the student books there is an accompanying Teacher's Guide (spiral bound, 8.5" x 11"). These includes advice for using the MOP curriculum, answers and instructional aids for every activity in the student book, supplemental discussions on pedagogic practices, and removable, photocopy-ready answer sheets for students to use with the activities.

1: Motion

Activities & Reader (ISBN 0-7872-3927-5, 190 pages)

How to Use This Book    xi

Acknowledgments    xiii

Activities

  • 1 - Looking Ahead    1
  • 2 - Communicating the Position of an Object    3
  • 2A - Communicating the Position of an Object (Alternative Version)    7
  • 3 - Describing Position    9
  • 4 - Using Graphs of Position vs. Time    15
  • 5 - Generating Sketches of Position vs. Time    19
  • 6 - Translating Graphs of Position vs. Time    23
  • 7 - Describing Displacement    27
  • 8 - Describing Velocity    31
  • 9 - Using Graphs of Velocity vs. Time    35
  • 10 - Generating Sketches of Velocity vs. Time    39
  • 11 - Translating Graphs of Velocity vs. Time    43
  • 12 - Relating Strobe Diagrams to Plots of Position vs. Time and Velocity vs. Time    47
  • 13 - Finding and Comparing Velocities    53
  • 14 - Relating Graphs of Position vs. Time and Velocity vs. Time    57
  • 15 - More Relating Graphs of Position vs. Time and Velocity vs. Time    61
  • 16 - Solving Constant-Velocity Problems Using Different Methods    65
  • 17 - Solving Constant-Velocity Problems    69
  • 18 - Recognizing Accelerated Motion    73
  • 19 - Describing Changes in Velocity    75
  • 20 - Recognizing Graphs of Acceleration vs. Time    81
  • 21 - Generating Sketches of Acceleration vs. Time    85
  • 22 - Translating Graphs of Acceleration vs. Time    87
  • 23 - Calculating Average Acceleration    89
  • 24 - Relating Strobe Diagrams to Graphs of Acceleration vs. Time    93
  • 25 - Relating Graphs and Kinematic Functions    97
  • 26 - Relating Kinematic Quantities with Kinematic Functions    101
  • 27 - Relating Graphs of Position, Velocity, and Acceleration vs. Time    105
  • 28 - Comparing Graphs of Velocity vs. Time and Displacement vs. Time    109
  • 29 - Translating Between Different Representations of Accelerated Motion    111
  • 30 - Graphical Representations of Motion: Reflection and Integration    115
  • 31 - Evaluating Procedures for Solving Kinematics Problems    119
  • 32 - Executing Procedures for Solving Kinematics Problems    125
  • 33 - Generating Procedures for Solving Kinematics Problems    127
  • 34 - Solving Constant-Acceleration Problems    129
  • 35 - Summarizing and Structuring Kinematics Ideas    133

Reader: Chapter 1—Describing Motion    R1

  • 1.0 Introduction    R1
    • six terms used to describe motion    R1
  • 1.1 Position    R1-5
    • Describing the position of an object    R1-4
      • definition of the term origin    R1
      • units of position: meter (m), kilometer (km), and centimeter (cm)    R2
      • three representations for position    R2
        • magnitude & direction representation    R2
        • component representation    R3
        • directed line segment representation    R3
      • representing the position in two dimensions    R3
        • magnitude & direction    R3,4
        • component representation    R4
        • directed line segment    R4
      • why we use three different representations    R4
    • Using graphs to describe the position of objects moving in one dimension    R5
  • 1.2 Displacement    R6,7
    • Introduction    R6
    • Displacement in one dimension    R6,7
      • symbol for displacement: "delta-x"    R6
      • definition of displacement    R6
      • an example of displacement in all three representations    R6,7
    • Displacement in two dimensions    R7
  • 1.3 Velocity    R8-18
    • Introduction    R8,9
      • difference between speed and velocity    R8
      • how we recognize when something has a velocity    R8
      • definition of average velocity (in one dimension)    R8
      • definition of velocity (or instantaneous velocity)    R9
      • definition of speed    R9
    • Representing velocity (in two dimensions)    R9-11
      • using all three representations for velocity    R10
      • how to estimate the components of velocity using a directed line segment    R11
    • Representing velocity at different times (in one dimension)    R12
    • Relationships between graphs of position and velocity    R12-15
      • constant, positive velocity    R13
      • constant, negative velocity    R13
      • changing velocity    R14
      • meaning of the area below velocity vs. time    R14
      • graphs of position vs. time    R15
      • meaning of the slope of position vs. time    R15
    • Using algebra to relate position and velocity    R16,17
      • equation for displacement when velocity is constant    R17
      • equation for position vs. time when velocity is constant    R17
    • Avoiding pitfalls when working with velocity concepts    R18,19
      • definition of average speed    R18
      • why the average speed for a trip is not the average of the speeds during the trip    R18
      • why the average speed for a trip is not the magnitude of the average velocity    R18,19
  • 1.4 Acceleration    R19-33
    • Introduction    R19-21
      • how the term acceleration is used in physics compared to how the term is used in everyday language    R19
      • four examples of motion:    R19-21
        • a car moving at constant velocity    R19
        • a car with changing speed but constant direction    R20
        • a car with constant speed but changing direction    R20
        • a thrown ball has changing speed and direction    R21
    • Defining acceleration for straight-line motion (motion in one dimension)    R21-24
      • symbol for acceleration: ax    R21
      • definition of average acceleration    R21
      • why "negative acceleration" does not mean "slowing down"    R22,23
      • definition of acceleration (or instantaneous acceleration)    R24
    • Representing and interpreting acceleration in one dimension    R24,25
      • using directed line segments for velocity    R24
      • using a number line for velocity    R25
    • Relationships between graphs of acceleration, velocity, and position (vs. time)    R26-28
      • calculations of the slopes of tangent lines    R26
      • verification that the slope of position vs. time is the velocity    R26,27
      • meaning of the slope of velocity vs. time    R27
      • meaning of the area below acceleration vs. time    R28
    • Deriving the kinematic equations for constant acceleration    R28-33
      • acceleration = 0    R29
        • how to find the displacement using a velocity graph    R29
        • equation for the position at time t    R29
      • acceleration <> 0    R30-33
        • how to find velocity using an acceleration graph    R30
        • equation for the velocity at time t    R30
        • how to find position using a velocity graph    R31
        • equation for the position at time t for constant acceleration    R31
        • equation for the squared velocity after displacement "delta-x"    R31
        • how to use graphs to solve problems    R32,33
  • 1.5 Kinematics    R34-36
    • Introduction    R34
    • Definitions    R34
      • position    R34
      • displacement    R34
      • average velocity    R34
      • velocity    R34
      • speed    R34
      • average speed    R34
      • average acceleration    R34
      • acceleration    R34
    • Relationships between graphs of motion quantities    R35
      • meaning of the slope of position vs. time    R35
      • meaning of the slope of velocity vs. time    R35
      • meaning of the area below velocity vs. time    R35
      • meaning of the area below acceleration vs. time    R35
      • diagrammatic representation of these relationships    R35
    • Derived equations relating the motion quantities (for constant acceleration)    R35
      • equation for the velocity at time t    R35
      • equation for the position at time t    R35
      • equation for the squared velocity after displacement "delta-x"    R35
      • definitions of symbols used in these derived equations    R35
    • Conclusion    R36
      • why problem solving is so difficult    R36
      • how to simplify kinematics problems    R36
      • why understanding motion is so important    R36

1-TG: Teacher's Guide to Motion

(ISBN 0-7872-3928-3, 354 pages)
A Letter from the Authors vii
Getting Started with Minds•On Physics xi
Answers & Instructional Aids for Teachers 1
1Looking Ahead1
2Communicating the Position of an Object7
2ACommunicating the Position of an Object (Alternative Version)9
3Describing Position11
4Using Graphs of Position vs. Time17
5Generating Sketches of Position vs. Time23
6Translating Graphs of Position vs. Time29
7Describing Displacement33
8Describing Velocity39
9Using Graphs of Velocity vs. Time45
10Generating Sketches of Velocity vs. Time51
11Translating Graphs of Velocity vs. Time57
12Relating Strobe Diagrams to Plots of Position vs. Time and Velocity vs. Time63
13Finding and Comparing Velocities73
14Relating Graphs of Position vs. Time and Velocity vs. Time77
15More Relating Graphs of Position vs. Time and Velocity vs. Time83
16Solving Constant-Velocity Problems Using Different Methods87
17Solving Constant-Velocity Problems93
18Recognizing Accelerated Motion97
19Describing Changes in Velocity101
20Recognizing Graphs of Acceleration vs. Time109
21Generating Sketches of Acceleration vs. Time115
22Translating Graphs of Acceleration vs. Time121
23Calculating Average Acceleration127
24Relating Strobe Diagrams to Graphs of Acceleration vs. Time133
25Relating Graphs and Kinematic Functions141
26Relating Kinematic Quantities with Kinematic Functions149
27Relating Graphs of Position, Velocity, and Acceleration vs. Time157
28Comparing Graphs of Velocity vs. Time and Displacement vs. Time167
29Translating Between Different Representations of Accelerated Motion173
30Graphical Representations of Motion: Reflection and Integration183
31Evaluating Procedures for Solving Kinematics Problems187
32Executing Procedures for Solving Kinematics Problems191
33Generating Procedures for Solving Kinematics Problems195
34Solving Constant-Acceleration Problems199
35Summarizing and Structuring Kinematics Ideas205
Supplement A. Collaborative Group Techniques A1-A4
Supplement B. Concept-Based Problem Solving: Combining educational research results and practical experience to create a framework for learning physics and to derive effective classroom practices B1-B26
Supplement C. A Comparison of the Minds•On Physics Approach with the NRC's National Science Education Standards C1-C10
Answer Sheets end

2: Interactions

Activities & Reader (ISBN 0-7872-3929-1, 224 pages)

How to Use this Book    xi

Acknowledgments    xiii

Activities

  • 36 - Introducing Vectors    137
  • 37 - Representing Vectors Using Components    145
  • 38 - Changing Vector Representations    149
  • 39 - Adding Vectors    155
  • 40 - Finding Changes in Vector Quantities    161
  • 41 - Recognizing Interactions    165
  • 42 - Identifying Interactions    169
  • 43 - Interpreting Measurements of Forces    173
  • 44 - More Interpreting Measurements of Forces    179
  • 45 - Recognizing Forces in Realistic Situations    185
  • 46 - Comparing Magnitudes of Forces    191
  • 47 - More Comparing Magnitudes of Forces    195
  • 48 - Understanding Friction Forces    199
  • 49 - Calculating Forces Using Empirical Laws    205
  • 50 - Recognizing and Interpreting Free-Body Diagrams    209
  • 51 - Drawing and Using Free-Body Diagrams    215
  • 52 - Analyzing Physical Situations Using Free-Body Diagrams    223
  • 53 - Describing Physical Situations Using Free-Body Diagrams    227
  • 54 - Summarizing and Structuring Interactions    233
  • 55 - Analyzing Physical Situations Using Newton's First and Second Laws    235
  • 56 - More Analyzing Physical Situations Using Newton's First and Second Laws    243
  • 57 - Relating the Forces Exerted on an Object to its Motion    247
  • 58 - Making Distinctions Between Newton's Second and Third Laws    251
  • 59 - Reasoning with Newton's Laws    257
  • 60 - More Reasoning with Newton's Laws    261
  • 61 - Using Newton's Laws to Determine the Magnitudes and Directions of Forces    267
  • 62 - Solving Problems with Newton's Laws    273
  • 63 - Analyzing Forces without Empirical Laws    277
  • 64 - Calculating the Values of Physical Parameters and Quantities    281
  • 65 - Labeling Parts of Solutions and Executing Solution Plans    285
  • 66 - Developing Solution Plans and Solving Force Problems    293
  • 67 - Solving Force Problems: Reflection and Integration    297
  • 68 - Summarizing and Structuring Dynamics    301
  • 69 - Going Beyond Newton's Laws    303
  • 70 - Looking for New Principles    307

Reader: Chapter 2 — Describing Interactions

  • 2.0 Introduction    R37
    • What is meant by dynamics?    R37
    • Why is acceleration such an important concept?    R37
  • 2.1 INTERACTIONS AND FORCES    R37-46
    • Interactions    R37
      • how to tell when two objects are interacting    R37
      • What if the effect is not visible?    R37
    • Forces    R37,38
      • relationship between interactions and forces    R37
      • many different ways to say that two objects are interacting    R38
      • how a force might change during a time interval    R38
    • Measuring forces    R38
      • explaining why springs are preferred for measuring forces    R38
      • importance of knowing what a scale is actually measuring    R38
    • Units of force    R38
      • introducing the pound (lb) and the newton (N)    R38
      • converting from one unit of force to another    R38
    • Identifying forces    R39-41
      • identifying the objects interacting    R39
      • identifying the type of interaction    R39,40
      • determining the direction of a force    R40,41
    • Empirical force laws    R41,42
      • What is meant by an empirical force law?    R41
      • features common to all empirical laws    R41
      • Table I: Summary of the empirical laws for common forces    R42
      • role of magnitude vs. direction in the empirical laws    R42
    • Fundamental laws for forces vs. empirical laws    R42,43
      • What is meant by a fundamental force law?    R42
      • the process of determining empirical force laws    R42,43
      • limitations of empirical laws    R43
    • Fundamental laws for forces    R43
      • the fundamental forces covered in this course    R43
      • Table II: Summary of the fundamental laws for two common forces    R43
    • Free-body diagrams: A way to help us inventory forces    R44,45
      • the thinking behind a free-body diagram    R44
      • some valid free-body diagrams    R44
      • features of a free-body diagram    R44,45
      • optional features of a free-body diagram    R45
      • guidelines for drawing a free-body diagram    R45
    • The net force    R46
      • definition of net force    R46
  • 2.2 NEWTON'S LAWS OF MOTION    R47-52
    • Mass vs. weight    R47,48
      • definition of weight    R47
      • how to measure the weight of something    R47
      • definition of mass    R47
      • how to measure the mass of something    R47
      • comparing the mass and the weight on the earth versus on the moon    R47,48
      • gravitational mass versus inertial mass    R48
    • Newton's three laws of motion    R48-50
      • Newton's first law of motion    R48
        • verbal statement of Newton's 1st law    R48
        • definition of net force    R48
      • Newton's second law of motion    R49
        • verbal statement of Newton's 1st law    R49
        • mathematical statement of Newton's 1st law    R49
        • definitions of inertial mass and gravitational mass    R49
        • definition of equilibrium    R49
      • Newton's third law of motion    R50
        • verbal statement of Newton's 3rd law    R50
        • mathematical statement of Newton's 3rd law    R50
        • relationship between forces and interactions    R50
        • explanation of the terms action and reaction    R50
        • difference between a reaction force and a balancing force    R50
    • Newton's laws and reference frames    R50,51
      • confirming Newton's laws using a constant-velocity frame    R50
      • contradicting Newton's laws using an accelerating frame    R50
      • definition of inertial frame    R51
    • Newton's laws and free-body diagrams    R51,52
      • Newton's 2nd law in component form    R51
      • applying the definition of the net force using components    R52
  • 2.3 DYNAMICS    R52-60
    • An agenda for dynamics    R52,53
    • Kinematics versus dynamics    R53
    • Reasoning with Newton's laws    R53-56
      • equilibrium situations (net force is zero)    R54,55
      • non-equilibrium situations (net force is not zero)    R56
    • Solving problems with Newton's laws    R56-59
      • goal of this approach to learning physics    R56
      • importance of analysis and reasoning skills    R56
      • role of analysis and reasoning while problem solving    R56-58
      • overview of problem solving in physics    R59
      • diagrammatic representation of the problem-solving process    R59
      • meaning of the diagrammatic representation    R59
    • Summary    R59
    • Limitations of dynamics    R59,60
      • conditions needed to solve dynamics problems    R59
      • some situations in which the motion cannot be determined using dynamics alone    R60
    • Conclusion    R60

Appendix: Table of Common Forces

  • Contact Forces    A1-4
    • Normal force    A1
    • Tension force    A1
    • Spring force (also called Elastic force)    A2
    • Buoyant force    A2
    • Friction forces    A3
      • kinetic    A3
      • static    A3
    • Air resistance force (also called Drag force)    A4
  • Action-at-a-distance Forces    A5,6
    • Gravitational force    A5
      • near the surface of the Earth    A5
      • Universal Law of Gravitation    A5
    • Electrostatic force    A6
    • Magnetic force    A6

2-TG: Teacher's Guide to Interactions

(ISBN 0-7872-3930-5, 372 pages)
Overview of the Minds•On Physics Materials vii
How to Use This Book ix
Answers & Instructional Aids for Teachers: 211
36Introducing Vectors211
37Representing Vectors Using Components221
38Changing Vector Representations225
39Adding Vectors231
40Finding Changes in Vector Quantities239
41Recognizing Interactions249
42Identifying Interactions255
43Interpreting Measurements of Forces261
44More Interpreting Measurements of Forces267
45Recognizing Forces in Realistic Situations275
46Comparing Magnitudes of Forces283
47More Comparing Magnitudes of Forces289
48Understanding Friction Forces295
49Calculating Forces Using Empirical Laws303
50Recognizing and Interpreting Free-Body Diagrams311
51Drawing and Using Free-Body Diagrams319
52Analyzing Physical Situations Using Free-Body Diagrams327
53Describing Physical Situations Using Free-Body Diagrams335
54Summarizing and Structuring Interactions343
55Analyzing Physical Situations Using Newton's First and Second Laws351
56More Analyzing Physical Situations Using Newton's First and Second Laws365
57Relating the Forces Exerted on an Object to its Motion375
58Making Distinctions Between Newton's Second and Third Laws381
59Reasoning with Newton's Laws389
60More Reasoning with Newton's Laws395
61Using Newton's Laws to Determine the Magnitudes and Directions of Forces403
62Solving Problems with Newton's Laws411
63Analyzing Forces without Empirical Laws421
64Calculating the Values of Physical Parameters and Quantities427
65Labeling Parts of Solutions and Executing Solution Plans433
66Developing Solution Plans and Solving Force Problems445
67Solving Force Problems: Reflection and Integration455
68Summarizing and Structuring Dynamics459
69Going Beyond Newton's Laws465
70Looking for New Principles471
Answer Sheets end

3: Conservation Laws & Concept-Based Problem Solving

Activities & Reader (ISBN 0-7872-3931-3, 224 pages)

How to Use this Book    xiii

Acknowledgments    xv

Activities

  • 71 - Investigating Collisions in which Two Objects Stick Together    313
  • 72 - Introducing the Concepts of Impulse and Momentum    317
  • 73 - Using Impulse and Momentum to Solve Constant-Force Problems    321
  • 74 - Analyzing Collisions Using Newton's Third Law    325
  • 75 - Relating Momentum Ideas to One-Body Problem Situations    331
  • 76 - Relating Momentum Ideas to Situations Having Two or More Objects    335
  • 77 - Reasoning with Impulse and Momentum Ideas    339
  • 78 - Solving Problems Using Momentum Principles    343
  • 79 - Summarizing and Structuring Momentum and Impulse Ideas    347
  • 80 - Recording Your Thoughts about Energy    349
  • 81 - Relating Forces to the Motion of Objects    353
  • 82 - Relating Work to Forces and Displacements    357
  • 83 - Recognizing the Presence of Work    361
  • 84 - Comparing the Work Done by Forces    367
  • 85 - Computing the Work Done by Forces    371
  • 86 - Recognizing and Comparing Kinetic Energy    375
  • 87 - Reasoning with Work and Energy Ideas    381
  • 88 - Solving Problems with the Work-Kinetic Energy Theorem    385
  • 89 - Recognizing the Presence of Potential Energy    389
  • 90 - Comparing the Potential Energy    393
  • 91 - Computing the Potential Energy    399
  • 92 - Keeping Track of Energy: The Law of Conservation of Energy    403
  • 93 - Reasoning with Energy Ideas    411
  • 94 - Solving Problems Using Energy Ideas    415
  • 95 - Summarizing and Structuring Energy Ideas    419
  • 96 - Recording Your Ideas about Problem Solutions    421
  • 97 - Recognizing the Appropriate Principle/Law    425
  • 98 - Matching Solution Strategies with Problems    433
  • 99 - Writing and Comparing Solution Strategies    437
  • 100 - Solving One-Principle Problems    441
  • 101 - Solving More Complex Problems    445
  • 102 - Structuring Mechanics    449

Reader: Chapter 3 — Conservation Laws

  • 3.0 Introduction    R61
    • What is meant by a conservation law?    R61
    • Why use a conservation law instead of dynamics?    R61
  • 3.1 SYSTEMS    R61
    • What is a system?    R61
    • Sizes of systems    R61
  • 3.2 MOMENTUM AND IMPULSE    R62-65
    • Impulse    R62,63
      • definition of impulse for constant force    R62
      • units for impulse: N-s    R62
      • how to calculate impulse for a given force and time interval    R62,63
      • definition of net impulse for constant net force    R63
      • how to calculate net impulse for constant net force    R63
    • Momentum    R64,65
      • definition of momentum for single bodies    R64
      • how to calculate the momentum    R64
      • units for momentum: kg-m/s    R64
      • what momentum means in some common situations    R64
      • how to find the change in momentum    R64,65
  • 3.3 TWO PRINCIPLES FOR DESCRIBING PHYSICAL SYSTEMS AND SOLVING PROBLEMS    R66-70
    • Impulse-Momentum Theorem    R66,67
      • comparing the net impulse and the change in momentum    R66
      • equivalence of the units for impulse and the units for momentum    R66
      • statement of the Impulse-Momentum Theorem for single bodies    R66
    • Conservation of Momentum for two-body systems    R68-70
      • using Newton's third law to understand collisions    R68
      • using the Impulse-Momentum Theorem to understand collisions    R69
      • statement of Conservation of Momentum for no net force on system    R69
      • definition of total momentum    R69
      • situations in which total momentum is only approximately conserved    R69,70
  • 3.4 USING MOMENTUM IDEAS AND PRINCIPLES TO ANALYZE SITUATIONS AND SOLVE PROBLEMS    R70-79
    • Reasoning with momentum ideas    R70-74
      • situations involving a net impulse    R70-73
        • using the Impulse-Momentum Theorem when there is a net impulse    R71
        • looking at the change in momentum    R71
        • making reasonable assumptions before making comparisons    R72
        • using limiting cases to make comparisons    R72
        • effect of mass on an object's response to an interaction    R73
      • situations in which the net impulse is zero or very close to zero    R73,74
        • using Conservation of Momentum when the impulse is small    R74
        • Conservation of Momentum is a vector equation    R74
    • Solving problems with momentum ideas    R75-78
      • using the Impulse-Momentum Theorem to solve problems    R75,76
        • two different ways of using the Impulse-Momentum Theorem    R75
        • Impulse-Momentum Theorem for constant net force    R75
        • four types of quantities: forces, time intervals, masses, velocities    R75
        • representation of problem solving using the Impulse-Momentum Theorem    R76
      • using Conservation of Momentum to solve problems    R76-78
        • four common steps for solving Conservation of Momentum problems    R76
        • Conservation of Momentum is a vector equation    R77,78
        • representation of problem solving using Conservation of Momentum    R78
    • Summary of momentum ideas and principles    R79
      • one new state quantity: momentum p    R79
      • two new process quantities: impulse J, and change in momentum Dp    R79
      • two new physical principles: the Impulse-Momentum Theorem and Conservation of Momentum    R79
      • new energy ideas: work, kinetic energy, potential energy    R79
      • limitations of momentum ideas    R79
  • 3.5 WORK AND KINETIC ENERGY    R80-90
    • Definition of work    R80-84
      • What factors affect the way a force changes the speed of something?    R80
      • definition of work for a constant force using the component of the force parallel to the displacement    R80
      • work is a scalar quantity    R81
      • units for work: J (joule)    R81
      • calculating the work done by a constant force    R81
      • how the work done can be negative    R81
      • What happens when the force is perpendicular to the displacement?    R81
      • circumstances when a different definition of work is needed    R82
      • definition of work for a constant force using the component of the displacement parallel to the force    R82
      • definition of total work    R83,84
    • Calculating the work done by common forces    R84-89
      • work done by the gravitational force    R84
        • depends on the mass, the gravitational constant (g), and the change in height    R84
        • why there is a minus sign in the expression    R84
      • work done by the normal force    R85,86
        • why the normal force often does no work on an object    R85
        • situations in which the normal force does work on an object    R85
        • the total work done by the normal force is always zero    R85
        • how the normal force can do no work even when it delivers an impulse    R86
      • work done by the tension force    R86,87
        • why the tension force often does no work on an object    R86
        • situations in which the tension force does work    R86,87
        • the total work done by the tension force is always zero    R87
      • work done by the friction force (static and kinetic)    R88
        • the static friction force can do work on isolated objects    R88
        • the static friction force can do no total work    R88
        • why we cannot calculate the work done by kinetic friction    R88
      • work done by the spring force    R89
        • using a graph of force vs. displacement to find the work done    R89
        • the graph of force vs. displacement is often a straight line    R89
    • Kinetic energy    R90,91
      • What changes when total work is done on an object?    R90
      • definition of kinetic energy    R90
      • circumstances under which the kinetic energy changes    R91
      • definition of total kinetic energy    R91
  • 3.6 TWO MORE PRINCIPLES FOR DESCRIBING PHYSICAL SYSTEMS AND SOLVING PROBLEMS    R92-99
    • Work-Kinetic Energy Theorem    R92-94
      • Statement of the Work-Kinetic Energy Theorem    R92
      • depends on the total work and the change in kinetic energy    R92
      • statement of the Work-Kinetic Energy Theorem for a system of objects    R92
      • depends on the total work and the change in total kinetic energy    R92
      • this is a scalar equation    R92
      • using the Work-Kinetic Energy Theorem to find the speed of something    R92,93
      • sometimes the forces doing work are hard to determine    R94
      • more reasons why we cannot calculate the work done by kinetic friction    R94
    • Conservation of Energy    R95-99
      • statement of the Law of Conservation of Energy    R95
      • why we need two new kinds of energy: potential energy and microscopic energy    R95
    • Potential energy    R95-98
      • change in gravitational potential energy    R95
      • gravitational potential energy for objects near the surface of celestial bodies    R95
      • using a reference height to determine the gravitational potential energy    R95
      • gravitational potential energy does not depend upon motion    R96
      • gravitational potential energy can be negative    R96
      • finding the potential energy stored in a spring    R97
      • factors affecting the spring potential energy    R97,98
      • the spring potential energy is always positive    R98
    • Microscopic vs. macroscopic energy    R98,99
      • definitions of the microscopic and macroscopic realms    R98
      • how energy is contained in the microscopic realm    R98,99
      • definition of total energy    R99
      • Law of Conservation of Energy    R99
  • 3.7 USING ENERGY IDEAS AND PRINCIPLES TO ANALYZE SITUATIONS    R100-105
    • Analyzing situations using the Work-Kinetic Energy Theorem    R100,101
      • whenever the kinetic energy of something changes, work is done    R100
      • difficulties in identifying the forces actually doing work    R100,101
      • similarities and differences between momentum and kinetic energy    R101
    • Analyzing situations using Conservation of Energy    R102-106
      • why the law is not particularly useful without modification    R102
      • Work-Energy Theorem (for a system of objects)    R102
      • definition of external work    R102
      • different ways of looking at the same situation    R102-104
      • using dynamics and kinematics to analyze a situation before applying Conservation of Energy    R104
      • where the energy goes during a collision    R104,105
      • change in microscopic energy due to friction    R105
      • different situations that may be used to derive the change in microscopic energy due to friction    R105
      • change in microscopic energy due to air resistance    R106
  • 3.8 USING ENERGY IDEAS AND PRINCIPLES TO SOLVE PROBLEMS    R106-113
    • Solving problems using the Work-Kinetic Energy Theorem    R106-109
      • two procedures for solving problems    R106-108
      • representation of problem solving using the Work-Kinetic Energy Theorem    R108,109
    • Solving problems using Conservation of Energy    R109-113
      • similarities and differences between the Work-Kinetic Energy Theorem and the Work-Energy Theorem    R109
      • problems in which the total work done by external forces is zero or negligibly small    R110,111
      • problem in which the total work done by external forces in non-zero    R112
      • why the Work-Energy Theorem is how we apply Conservation of Energy to a system of objects    R113
      • representation of problem solving using Conservation of Energy    R113
    • Summary of energy ideas and principles    R113
      • many new state quantities: kinetic, potential, and microscopic energy    R113
      • many new process quantities: work, changes in state quantities    R113
      • one new physical law: Conservation of Energy    R113
      • two new problem-solving principles: the Work-Kinetic Energy Theorem and the Work-Energy Theorem    R113
    • Summary of conservation laws    R113-114
      • reasons for using conservation laws    R113
      • how scientists apply conservation laws to new situations    R114
      • what we will do as we study new areas of physics    R114

Reader: Chapter 4 — Concept-Based Problem Solving

  • 4.0 Introduction    R115
    • Some questions you might ask yourself before solving a problem    R115
    • Why a conceptual analysis should precede equation manipulation    R115
  • 4.1 A PHYSICIST'S VIEW OF MECHANICS    R116-121
    • Explanation    R116
      • What is meant by a "view of mechanics"    R116
      • what is meant by an "organizational structure"    R116
      • what motivates a physicist's organizational structure    R116
    • Prioritizing ideas in mechanics    R116-120
      • chronological list of many of the physics concepts learned so far    R116
      • physical principles, the most widely useful ideas in physics    R117
      • concepts, the ideas needed to understand principles    R117
      • equations, the relationships needed to apply concepts and principles (physical laws, definitions, empirical laws, and derived relations)    R117,118
      • a priority scheme for physics ideas, with examples    R118,119
      • other ideas relevant for solving problems (mathematical principles, operations, and problem-solving techniques)    R119,120
    • Interconnecting ideas in mechanics    R121
      • using concepts to organize knowledge    R121
  • 4.2 CONCEPT-BASED PROBLEM SOLVING    R121-126
    • How to start solving a problem    R121-123
      • the first three steps of concept-based problem solving    R121,122
        • step 1: sort the principles    R121,122
        • step 2: choose a principle    R122
        • step 3: apply the chosen principle and solve for the unknown    R122
      • solution to the sample problem    R122,123
    • How to finish solving a problem    R124-126
      • four suggestions for efficient and effective problem solving    R124,125
        • create sketches and diagrams    R124
        • count the number of equations and unknowns    R124
        • challenge your assumptions    R124,125
        • check your answer    R125,126
    • Conclusion    R126
      • representation of the concept-based problem-solving approach    R126

3-TG: Teacher's Guide to Conservation Laws & Concept-Based Problem Solving

(ISBN 0-7872-3932-1, 380 pages)
Overview of the Minds•On Physics Materials vii
How to Use This Book ix
Answers & Instructional Aids for Teachers 483
71Investigating Collisions in which Two Objects Stick Together483
72Introducing the Concepts of Impulse and Momentum491
73Using Impulse and Momentum to Solve Constant-Force Problems497
74Analyzing Collisions Using Newton's Third Law507
75Relating Momentum Ideas to One-Body Problem Situations517
76Relating Momentum Ideas to Situations Having Two or More Objects525
77Reasoning with Impulse and Momentum Ideas535
78Solving Problems Using Momentum Principles543
79Summarizing and Structuring Momentum and Impulse Ideas553
80Recording Your Thoughts about Energy561
81Relating Forces to the Motion of Objects567
82Relating Work to Forces and Displacements575
83Recognizing the Presence of Work581
84Comparing the Work Done by Forces589
85Computing the Work Done by Forces597
86Recognizing and Comparing Kinetic Energy605
87Reasoning with Work and Energy Ideas615
88Solving Problems with the Work—Kinetic Energy Theorem625
89Recognizing the Presence of Potential Energy635
90Comparing the Potential Energy641
91Computing the Potential Energy651
92Keeping Track of Energy: The Law of Conservation of Energy659
93Reasoning with Energy Ideas671
94Solving Problems Using Energy Ideas685
95Summarizing and Structuring Energy Ideas699
96Recording Your Ideas about Problem Solutions711
97Recognizing the Appropriate Principle/Law715
98Matching Solution Strategies with Problems725
99Writing and Comparing Solution Strategies735
100Solving One-Principle Problems745
101Solving More Complex Problems753
102Structuring Mechanics765
Answer Sheets end

FF: Fundamental Forces & Fields

Activities & Reader (ISBN 0-7872-5412-6, 207 pages)

How to Use this Book    xv

Acknowledgments    xvii

Activities

  • FF·1 - Exploring Models of Electromagnetism    1
  • FF·2 - Using a Model to Interpret, Explain, and Predict    7
  • FF·3 - Investigating Electrical Properties of Materials    13
  • FF·4 - Reasoning with a Model for Electrical Interactions    17
  • FF·5 - Exploring the Magnetic Interaction    21
  • FF·6 - Modeling the Magnetic Properties of Materials    25
  • FF·7 - Modeling the Magnetic Properties of Moving Charges    29
  • FF·8 - Reasoning with a Model for Magnetic Interactions    35
  • FF·9 - Exploring the Gravitational Interaction    39
  • FF·10 - Exploring the Idea of Weight    43
  • FF·11 - Distinguishing Mass and Weight    47
  • FF·12 - Modeling Universal Gravitation    51
  • FF·13 - Using a Mathematical Model for the Electric Force    55
  • FF·14 - Applying Coulomb's Law to Continuous Distributions of Charge    59
  • FF·15 - Estimating Electric Forces Using Coulomb's Law    65
  • FF·16 - Reasoning with Coulomb's Law    69
  • FF·17 - Developing an Empirical Force Law for Magnets    73
  • FF·18 - Using the Universal Law of Gravitation    79
  • FF·19 - Applying Universal Gravitation to Large-Scale Objects    83
  • FF·20 - Reasoning with Universal Gravitation    87
  • FF·21 - Mapping Magnetic Fields    91
  • FF·22 - Representing the Electric Field    97
  • FF·23 - Representing the Electric Field as a Vector Field    101
  • FF·24 - Investigating the Gravitational Field    107
  • FF·25 - Representing Vector Fields Using Field Line Diagrams    111
  • FF·26 - Applying Newton's Laws    117
  • FF·27 - Applying Work and Energy Ideas    121
  • FF·28 - Solving Problems Using Work and Energy Ideas    127
  • FF·29 - Summarizing and Structuring the Fundamental Forces    131

Reader: Fundamental Forces and Fields

  • 0. Introduction    R1
    • what is meant by a fundamental force    R1
    • a list of the fundamental forces    R1
    • some examples of what the fundamental forces are responsible for    R1
    • the organization of the Reader    R1
  • 1. QUALITATIVE DESCRIPTIONS OF FUNDAMENTAL FORCES    R1-20
    • 1.1. Modeling interactions    R2
      • what is meant by the term model    R2
      • goal of a model    R2
      • graphic representation of modeling    R2
    • 1.2. Electric phenomena    R2,3
      • examples of electric phenomena    R2
      • table showing how rubbed objects interact with each other    R3
      • introducing electric charge to explain pattern of electric phenomena    R3
      • defining which objects are said to be positive, which are negative, and which are neutral    R3
    • 1.3. Reasoning about electric interactions    R4
      • an example showing how we can predict the behavior of something    R4
      • an example showing the limitations of our current model    R4
    • 1.4. A simplified model of electric interactions    R4-6
      • goal of our simplified model    R4
      • assumption 1: All matter is made up of sub-microscopic particles    R5
      • assumption 2: These particles have mass and charge    R5
      • assumption 3: "Like" charges repel; "opposite" charges attract; neutral particles do not interact    R5
      • assumption 4: Everyday objects are neutral    R6
      • assumption 5: Charges can be transferred    R6
      • assumption 6: Electric interactions occur when one or both objects have excess charge    R6
      • assumption 7: Charge is conserved    R6
      • assumption 8: The mass of sub-microscopic particles is very small    R6
      • assumption 9: When styrofoam is rubbed with fur, the fur is defined to be positive, and the styrofoam is defined to be negative    R6
    • 1.5. Applying the simplified model of electric interactions    R7
      • An example showing how the model can predict the behavior of something    R7
    • 1.6. The atomic model of matter    R7,8
      • types of charge on the proton, neutron, and electron    R7
      • how the atomic model will and will not be used    R8
    • 1.7. A model of the electrical properties of materials    R8,9
      • goal of our model of electrical properties of materials    R8
      • assertion 1: Only electrons can be transferred by rubbing    R8
      • assertion 2: Excess electrons on a conductor flow easily    R8
      • why some electrical demonstrations give inconsistent results    R8
      • assertion 3: Excess electrons on an insulator do not flow very easily    R9
      • assertion 4: Some electrons in a conductor are relatively free to move    R9
      • conductors exchange electrons on contact    R9
      • assertion 5: Most electrons in an insulator are not relatively free to move    R9
      • assertion 6: The strength of the electric force depends on charge separation    R9
    • 1.8. Applying the atomic model of electric interactions    R10,11
      • explaining why neutral objects are attracted to charged objects    R10
      • predicting the charges on pie plates    R11
    • 1.9. Magnetic phenomena    R11,12
      • what is meant by a permanent magnet    R11
      • what is meant by the poles of a magnet    R11
      • what is meant by the North (N) and South (S) poles of a magnet    R11
      • table showing how different materials interact magnetically    R12
      • other properties of interacting materials    R12
    • 1.10 Modeling the magnetic interaction    R12-14
      • what is meant by a nanomagnet    R13
      • assumption 1: All matter is made up of tiny nanomagnets    R13
      • assumption 2: "Like" poles repel; "opposite" poles attract    R13
      • assumption 3: Every material's nanomagnets have a characteristic strength    R13
      • what is meant by magnetic materials    R13
      • assumption 4: The interaction of two nanomagnets depends on their strengths    R13
      • assumption 5: The interaction of two nanomagnets depends on their separation    R13
      • what is meant by non-magnetic materials    R13
      • how these assumptions are applied to different materials    R13
      • rough depictions of the nanomagnets in non-magnetic materials, magnetic materials, and permanent magnets    R14
      • what is meant by a magnetic domain    R14
    • 1.11 Applying our simplified model of magnetic interactions    R14
      • Examples of how to apply this model of magnetic interactions    R14
    • 1.12 An atomic model of magnetic interactions    R15
      • reasons we need to go to the atomic model    R15
      • two moving charges are needed for the magnetic interaction    R15
      • how to go from moving charges to nanomagnets    R15
    • 1.13 Applying the atomic model of magnetic interactions    R16
      • one more assumption: the strength of a nanomagnet is due primarily to an atom's orbiting electrons    R16
      • examples of how to apply the atomic model of magnetic interactions    R16
    • 1.14 "Local" gravitation    R17,18
      • what is meant by local gravitation    R17
      • how we know that gravitation is caused by the Earth    R17
      • what is meant by "local" gravitation on the Moon    R18
    • 1.15 Weight    R18
      • how weight might appear to be different for different observers    R18
      • definition of the term weight    R18
      • why a scale sometimes cannot be used to determine weight    R18
      • why air has weight    R18
    • 1.16 Mass vs. weight    R19
      • differences between mass and weight    R19
    • 1.17 "Universal" gravitation    R19,20
      • what is meant by Universal gravitation    R19
      • gravitational force as a function of position assuming the Earth has a uniform density    R19
      • comparison of the gravitational forces exerted by the Earth and the Moon    R20
      • why the local gravitational constant on the Moon is 1/6 that on the Earth    R20
      • summary of gravitation    R20
  • 2. MATHEMATICAL DESCRIPTIONS OF FUNDAMENTAL FORCES    R21-33
    • 2.1. Coulomb's law for electric forces    R21,22
      • what is meant by a point charge    R21
      • mathematical description of Coulomb's law    R21
      • how to find the direction of the electric force    R21
      • MKS unit of charge (the Coulomb, C)    R22
      • charges of the proton and electron    R22
      • an example of how to apply Coulomb's law    R22
    • 2.2. The Superposition Principle    R22,23
      • why we need the Superposition Principle    R22
      • verbal description of the Superposition Principle    R22
      • an example showing how to apply the Superposition Principle    R23
    • 2.3. Applying Coulomb's law to non-point objects    R24
      • force law when objects are far apart    R24
      • how to treat objects close together    R24
    • 2.4. Reasoning with Coulomb's law    R25,26
      • a convenient unit of charge is the microCoulomb (µC)    R25
      • 3 examples showing how to reason using Coulomb's law    R25,26
    • 2.5. Universal law of gravitation    R27,28
      • mathematical description of the Universal law of gravitation    R27
      • how to find the direction of the gravitational force    R27
      • an example showing how to apply the Universal law of gravitation    R27
      • an example showing how to apply the Superposition Principle    R28
    • 2.6. Applying Universal gravitation to non-point objects    R28,29
      • applying Universal gravitation when objects are far apart    R28
      • applying Universal gravitation when an object is close to a celestial body    R28,29
      • what is meant by a shell    R28
      • force law when object is outside the mass shell    R29
      • force law when object is inside the mass shell    R29
      • how to apply these results to celestial bodies such as the Earth and Moon    R29
    • 2.7. Astronomical data    R30
      • mass, average radius, average density, g on its surface, average orbital radius, and orbital period for the Earth, the Moon, and the Sun    R30
      • an example of how to use astronomical data    R30
    • 2.8. Deciding how to apply the Universal law of gravitation    R30,31
      • 3 general methods for applying the Universal law of gravitation    R30,31
      • an example showing how these methods apply to 6 situations    R31
    • 2.9. Reasoning with Universal gravitation    R32,33
      • examples showing how to reason using Universal gravitation    R32,33
    • 2.10 The magnetic interaction    R33
      • why we cannot provide a mathematical description of the magnetic interaction    R33
      • some features you should still know about the magnetic interaction    R33
  • 3. FIELDS    R34-45
    • some of the different ways the term field is used    R34
    • 3.1. Scalar vs. vector fields    R34
      • what is meant by a scalar field    R34
      • what is meant by a vector field    R34
      • temperature is a good example of a scalar field    R34
      • velocity of air currents is a good example of a vector field    R34
      • vector field diagram for air currents in a certain region of space    R34
    • 3.2. Fields for fundamental forces    R35
      • why we introduce fields for fundamental forces    R35
      • how a fundamental field is defined: in terms of the force exerted on an object    R35
      • what creates what types of fields    R35
    • 3.3. The electric field    R36
      • force on point charge q due to electric field E    R36
      • definition of the electric field    R36
      • using Coulomb's law to find the electric field created by a point charge    R36
      • finding the direction of the electric field    R36
      • how the mutual forces can be the same even though the fields are different    R36
    • 3.4. Electric field for multiple point charges    R37
      • an example of how to find the electric field for two point charges    R37
      • vector field diagrams for the "dipole" and "dicharge" distributions of charge    R37
    • 3.5. Electric field for a spherical shell of charge    R38
      • electric field inside a shell of charge    R38
      • electric field outside a shell of charge    R38
      • finding the direction of the electric field outside a shell of charge    R38
      • an example showing how to find the electric field on a rubber ball    R38
    • 3.6. The gravitational field    R39
      • why we use the same symbol for "local" and "Universal" gravitation    R39
      • definition of the gravitational field    R39
      • gravitational field created by a point mass    R39
      • how to find the direction of the gravitational field    R39
    • 3.7. Gravitational field for non-point masses    R39,40
      • using shells to find the gravitational field for a celestial body    R39
      • sketch of gravitational field strength g vs. distance from the center of the Earth    R40
      • finding and verifying the location between the Earth and the Moon where the gravitational field is zero    R40
    • 3.8. The magnetic field    R41
      • why we use a compass needle to determine the direction of the magnetic field    R41
      • magnetic field for a long, straight wire    R41
      • magnetic field for a loop of wire    R41
    • 3.9. Finding the magnetic field for other arrangements of current-carrying wire    R42
      • magnetic field for two parallel wires, with currents moving in opposite directions    R42
      • magnetic field for a coil of wire    R42
    • 3.10 Force on a point charge moving through a magnetic field    R42,43
      • diagram showing the orientations of the velocity v, magnetic field B, and magnetic force Fm    R42
      • 2 mathematical expressions for the magnetic force on charge q    R43
      • finding the direction of the magnetic force    R43
      • why we cannot write an expression for the magnetic field B created by a moving point charge    R43
    • 3.11 Limitations of vector field diagrams    R43
      • many reasons why vector field diagrams are sometimes not the best way to represent fields    R43
      • an example using the "dipole" arrangement of charges    R43
    • 3.12 Field line diagrams    R44
      • what is meant by a field line    R44
      • how to find the direction of the vector field using a field line    R44
      • field line diagrams are 3 dimensional    R44
      • drawing showing the field lines near a positive point charge    R44
      • how to find the comparative strength of the vector field using the density of field lines    R44
      • why we usually draw field line diagrams in only 2 dimensions    R44
      • limitations of the 2-dimensional field line diagram    R44
    • 3.13 Interpreting field line diagrams    R44,45
      • an example using a pair of point charges    R44,45
      • description of the field line diagram    R44
      • analysis of the field line diagram    R44,45
      • actual charge distribution used in this example    R45
    • 3.14 Reasoning with field line diagrams    R45
      • 3 conclusions that can be reached through reasoning    R45
        • - Field lines do not cross each other    R45
        • - Field lines are not the paths of objects    R45
        • - The field is not strongest near field lines    R45
  • 4. REASONING AND SOLVING PROBLEMS USING PHYSICAL LAWS    R46-53
    • a list of the useful concepts, principles, and models presented so far    R46
    • 4.1. Reasoning with Newton's laws    R46-48
      • how this part of the Reader will be different from earlier parts involving forces    R46
      • an example involving Newton's 2nd and 3rd laws, as well as momentum conservation    R47
      • an example involving our model of materials    R47
      • an example showing how diagrams can be useful    R48
    • 4.2. Solving problems using Newton's laws    R48,49
      • an example involving the magnetic interaction    R48,49
    • 4.3. Reasoning with energy ideas    R49-51
      • table showing the major energy principles, with related concepts and their definitions    R49
      • an example involving the Work-Energy Theorem    R50
      • an example involving the Work-Kinetic Energy Theorem    R50
    • 4.4. Solving problems using energy ideas    R51-53
      • the procedure for determining potential energy    R51
      • some common reference points    R51
      • finding the potential energy stored in the field of two point charges    R51
      • choosing the reference point for two point charges    R51
      • mathematical expression for the potential energy for two point charges    R51
      • mathematical expression for the potential energy for two point masses    R52
      • an example showing how to apply gravitational and electric potential energy    R52,53
      • 5 common steps needed to solve problems using energy ideas    R53

FF-TG: Teacher's Guide to Fundamental Forces & Fields

(ISBN 0-7872-3934-8, 458 pages)

Sorry, but we haven't posted the table of contents for this volume (yet). Contact Bill Leonard for assistance.

AT: Advanced Topics in Mechanics

Activities & Reader (ISBN 0-7872-5411-8, 172 pages)

How to Use this Book    xv

Acknowledgments    xvii

Activities

  • AT·1 - Exploring Ideas About Circular Motion    1
  • AT·2 - Finding Acceleration for Circular Motion    5
  • AT·3 - Finding Radial Acceleration for Circular Motion    9
  • AT·4 - Finding Tangential Acceleration for Circular Motion    13
  • AT·5 - Reasoning About Circular Motion    15
  • AT·6 - Solving Problems in Circular Motion    19
  • AT·7 - Exploring Ideas About Projectile Motion    23
  • AT·8 - Relating Kinematic Quantities for Two-Dimensional Motion    29
  • AT·9 - Reasoning About Projectile Motion    35
  • AT·10 - Solving Problems in Projectile Motion    39
  • AT·11 - Solving Problems in Two-Dimensional Motion    43
  • AT·12 - Exploring Ideas About Relative Motion    47
  • AT·13 - Exploring Relative Motion in Two Dimensions    51
  • AT·14 - Reasoning About Relative Motion    55
  • AT·15 - Solving Problems in Relative Motion    59
  • AT·16 - Graphing Rotational Motion    63
  • AT·17 - Introducing Rotational Kinematics    67
  • AT·18 - Solving Rotational Kinematics Problems    71
  • AT·19 - Introducing Rotational Dynamics    75
  • AT·20 - Solving Rotational Dynamics Problems    79
  • AT·21 - Identifying Energy in Rotational Systems    83
  • AT·22 - Solving Problems with Energy in Rotational Systems    87
  • AT·23 - Solving Problems in Rotational Motion    91

Reader: Advanced Topics in Mechanics

  • Chapter 1. Circular, Projectile & Relative Motion
    • 3 independent sections: circular motion, projectile motion & relative motion    R1
    • 1.1. CIRCULAR MOTION    R1-10
      • types of situations covered by circular motion    R1,2
      • 1.1.1. Uniform circular motion    R2-4
        • what is meant by "uniform" circular motion    R2
        • factors affecting acceleration: speed and radius of circle    R2
        • starting with the definition of acceleration    R2
        • diagram showing the change in velocity [delta]v for a small time period    R3
        • table showing the average acceleration for smaller and smaller time periods    R3
        • 1 effect of doubling the radius of the circular path    R3
        • 2 effects of doubling the speed of the ball    R3
        • magnitude of the acceleration for uniform circular motion    R4
        • direction of the acceleration for uniform circular motion    R4
      • 1.1.2. Newton's laws and uniform circular motion    R4
        • relationship between net force and acceleration    R4
      • 1.1.3. Non-uniform circular motion    R5,6
        • what is meant by "non-uniform" circular motion    R5
        • definition of the radial component of acceleration    R5
        • definition of the tangential component of acceleration    R5
        • magnitude of the radial component of acceleration for motion along any circle    R5
        • direction of the radial component of acceleration    R5
        • magnitude of the tangential component of acceleration for motion along any circle    R5
        • direction of the tangential component of acceleration    R5
        • finding the forces responsible for the radial and tangential accelerations    R5,6
      • 1.1.4. Motion along a curved path    R6,7
        • importance of finding circles that match the curvature of the path    R6
        • radial acceleration points toward the center of curvature    R6
        • radius of curvature is the radius of the matching circle    R7
        • magnitude of the radial component of acceleration for motion along any path    R7
        • direction of the radial component of acceleration    R7
      • 1.1.5. Reasoning with circular motion ideas    R7-9
        • only 2 new "big ideas" in circular motion    R7
        • integrating old ideas into new situations    R7
        • using a free-body diagram to analyze circular motion    R8
        • using energy ideas to analyze circular motion    R8,9
      • 1.1.6. Solving problems with circular motion ideas    R9,10
        • table of ideas and principles needed to solve circular motion problems    R9
        • example showing all the ideas that can impact a circular motion problem    R10
    • 1.2. PROJECTILE MOTION    R11-22
      • what is meant by projectile motion    R11
      • 1.2.1. Simple projectile motion    R11,12
        • what is meant by "simple" projectile motion    R11
        • an example using strobe diagram of a ball thrown into the air    R11,12
        • relationship of strobe diagram and plots to Newton's laws and force ideas    R12
        • using plots of vx and vy vs. time to find ax and ay    R12
      • 1.2.2. Algebraic representation of simple projectile motion    R12,13
        • using a graph to write an expression for horizontal position vs. time    R12
        • using a graph of velocity vs. time to derive expressions for vertical velocity vs. time and height vs. time    R12,13
      • 1.2.3. Algebraic representation of two-dimensional motion    R13
        • defining symbols for the vectors r, v, and a    R13
        • kinematic expressions for position and velocity as functions of time for constant acceleration    R13
      • 1.2.4. Free-fall acceleration    R14
        • difference between g and ag    R14
        • why we use the symbol ag to denote free-fall acceleration    R14
      • 1.2.5. Special features of simple projectile motion    R14
        • what is meant by the term trajectory    R14
        • 3 special features of a trajectory: time of flight, range, and maximum altitude    R14
        • labeled diagram of trajectory showing special features    R14
        • what the time of flight depends on    R14
        • what the range depends on    R14
        • what the maximum altitude depends on    R14
      • 1.2.6. Reasoning about simple projectile motion    R15-17
        • seeing patterns in how the speed and velocity of a projectile change    R15
        • comparing trajectories to understand projectile motion    R16
        • applying Newton's laws to projectile motion    R17
        • applying conservation of energy to projectile motion    R17
      • 1.2.7. Solving problems in simple projectile motion    R18-20
        • 4 relationships needed to solve problems in simple projectile motion    R18
        • 4 keys to solving projectile motion problems    R18,19
          • recognizing that time t is the same in all 4 relationships    R18
          • translating given information properly into equation form    R18
          • focusing on special features of trajectories    R18
          • realizing when you have enough equations to solve for the unknown    R18,19
        • 2 examples    R19,20
        • how to interpret a negative root    R20
      • 1.2.8. Solving problems in two-dimensional motion    R21,22
        • 4 relationships needed to solve problems in 2-dimensional motion    R21
        • 2 examples    R21,22
    • 1.3. RELATIVE MOTION    R23-35
      • situations covered by relative motion    R23
        • some goals of studying relative motion    R23
      • 1.3.1. Relative motion in one dimension    R23,24
        • 4 people at the airport on or near a moving walkway    R23
        • table of velocities as seen from 2 different perspectives    R24
      • 1.3.2. Reference frames    R24
        • what is meant by reference frame    R24
        • table of positions as measured in 2 different frames at <nobr>t = 0.0 s</nobr>    R24
        • why some positions change but other positions stay the same    R24
      • 1.3.3. Notation and language    R25
        • labeling frames as "primed" and "unprimed"    R25
        • labeling positions and velocities as "primed" and "unprimed"    R25
        • reasons someone's speed can be zero even though everyone agrees he is moving    R25
      • 1.3.4. Relative motion in two dimensions    R26
        • Jamal throws a ball into the air while riding a skateboard    R26
        • to Jamal, motion of the ball is 1-dimensional    R26
        • to Betty, motion of the ball is 2-dimensional    R26
      • 1.3.5. Position and velocity transformations    R26-29
        • a boat is crossing a river, while Sue is running along the shore    R26
        • in 2 dimensions, each reference frame has 2 coordinate axes    R26
        • graphical representation of position transformation    R26,27
        • numerical and symbolic representations of position transformation    R27
        • general expressions for transforming positions    R27
        • general expression for transforming velocity    R27
        • 3 representations of velocity transformation    R27
        • general expression for transforming acceleration    R28
        • 2 examples of velocity transformation    R28,29
      • 1.3.6. Newton's laws in different reference frames    R29,30
        • science experiments on a train moving with constant velocity relative to the ground    R29
        • laws of physics are the same in a frame moving with constant velocity    R29
        • science experiments on a train slowing down relative to the ground    R29,30
        • Newton's laws and empirical laws are different in an accelerating frame    R30
        • small accelerations have only small effects on Newton's laws    R30
        • definition of the phrase inertial frame    R30
      • 1.3.7. Conservation of energy in different reference frames    R30,31
        • throwing a ball from the ground and from a moving train    R30,31
        • change in kinetic energy depends on the frame of reference    R31
        • work done by a force depends on the frame of reference    R31
        • table showing how the scenarios look different in different frames    R31
      • 1.3.8. Reasoning with relative motion ideas    R32,33
        • only 3 new ideas    R32
          • the reference frame is the key to determining positions, velocities, and energy    R32
          • when the frames are inertial, forces, masses, and accelerations are the same in all frames    R32
          • there is no preferred reference frame    R32
        • sometimes, a situation is easier to analyze in one frame than another    R32,33
      • 1.3.9. Solving problems with relative motion ideas    R33-35
        • many common problems involve navigation    R33,34
        • definition of the term heading    R35
  • Chapter 2. Rotational Motion
    • situations covered by rotational motion    R36
    • how we are going to approach rotational motion    R36
    • why we are going to always use a fixed axis    R36
    • 3 main sections: angular kinematics, angular dynamics & energy in rotating systems    R36
    • 2.1. ANGULAR KINEMATICS    R37-42
      • what is meant by angular kinematics    R37
        • why we need to introduce a new set of kinematic quantities    R37
      • 2.1.1. Angular vs. linear kinematics    R37,38
        • description of linear motion    R37
        • description of angular motion    R37
        • what is meant by "CCW" and "CW"    R37
        • CCW rotations are positive    R37
        • table comparing linear motion and rotational motion (fixed axis)    R38
      • 2.1.2. The radian    R38,39
        • why the radian is different from other units of measure    R38
        • why the radian is the preferred unit for angles    R38
        • an example using arc length    R38,39
        • 2 examples applying the radian    R39
        • why certain relationships are not proper    R39
      • 2.1.3. Reasoning with angular kinematics ideas    R40,41
        • angular velocity and linear velocity are very different quantities    R40
        • linear velocity depends on your location on the spinning object    R41
        • the linear velocity can be zero even though the object is spinning    R41
      • 2.1.4. Solving problems in angular kinematics    R41,42
        • relationship between angular speed and angular velocity    R41
        • graphs can help organize information and help solve problems    R42
    • 2.2. ANGULAR DYNAMICS    R43-51
      • situations covered by angular dynamics    R43
      • 2.2.1. Pivots    R43
        • what is meant by pivot    R43
        • an example using a hinged door    R43
        • why we ignore forces parallel to the axis of rotation    R43
        • what is meant by "about the pivot" or "about the point p"    R43
      • 2.2.2. Torque    R44-46
        • 4 factors affecting the torque    R44
        • 2 definitions of torque for rotations about a fixed axis    R44
        • finding the direction of torque    R44
        • SI unit of torque (N·m)    R44
        • 2 examples    R45
        • definition of net torque for rotations about a fixed axis    R46
      • 2.2.3. Moment of inertia    R46,47
        • 3 factors affecting the moment of inertia    R46
        • definition of moment of inertia (point mass)    R46
        • definition of moment of inertia (composite object)    R46
        • 2 examples    R47
      • 2.2.4. Newton's 2nd law in rotational form    R48
        • mathematical description of Newton's 2nd law for rotations about a fixed axis    R48
      • 2.2.5. Angular vs. linear dynamics    R48
        • table comparing linear and angular dynamics    R48
      • 2.2.6. Reasoning with angular dynamics ideas    R48-50
        • for static situations, every axis is a fixed axis of rotation    R48,49
        • 3 examples    R49,50
        • the gravitational force acts "as though" through the center of gravity or balance point    R49
      • 2.2.7. Solving problems in angular dynamics    R51
        • an example    R51
        • relationship between angular acceleration and linear acceleration    R51
    • 2.3. ENERGY IN ROTATIONAL SYSTEMS    R52-56
      • 2.3.1. Kinetic energy of rotating objects    R52
        • rewriting the kinetic energy using rotational quantities    R52
      • 2.3.2. Potential energy in rotational systems    R52
        • how energy can be stored in a rotational system    R52
        • torque law for a torsional spring    R52
        • potential energy for a torsional spring    R52
      • 2.3.3. Energy for linear vs. rotational motion    R53
        • table comparing energy for linear and rotational motion    R53
        • why we do not refer to "angular energy"    R53
      • 2.3.4. Reasoning with energy ideas in rotational systems    R53,54
        • 2 examples    R53,54
        • importance of using the center of gravity in energy problems    R54
      • 2.3.5. Solving problems with energy ideas in rotational systems    R54-56
        • how conservation of energy and the Work-Kinetic Energy Theorem are applied    R54,55
        • why there is no such thing as "angular" energy    R55
        • 2 examples    R55,56
    • 2.4. SOLVING PROBLEMS IN ROTATIONAL MOTION    R56
      • general guidelines for solving problems in rotational motion    R56

AT-TG: Teacher's Guide to Advanced Topics in Mechanics

(ISBN 0-7872-5412-6)

Sorry, but we haven't posted the table of contents for this volume (yet). Contact Bill Leonard for assistance.

CS: Complex Systems

Activities & Reader (ISBN 0-7872-5413-4)

Sorry, but we haven't posted the table of contents for this volume (yet). Contact Bill Leonard for assistance.

CS-TG: Teacher's Guide to Complex Systems

(ISBN 0-7872-5414-2)

Sorry, but we haven't posted the table of contents for this volume (yet). Contact Bill Leonard for assistance.

Sample MOP Activities

Selected excerpts from the MOP curriculum

Below are links to a few of the "minds-on" activities we have developed, in PDF format. (Adobe Acrobat Reader or equivalent required.)

1: Motion (core activities 1-35)

1. Looking Ahead

4. Using Graphs of Position vs. Time

11. Translating Graphs of Velocity vs. Time

16. Solving Constant-Velocity Problems Using Different Methods

2: Interactions (core activities 36-70)

41. Recognizing Interactions

46. Comparing Magnitudes of Common Forces

50. Recognizing and Interpreting Free-Body Diagrams

59. Reasoning With Newton's Laws

3: Conservation Laws & Concept-Based Problem Solving (core activities 71-102)

77. Reasoning with Impulse and Momentum Ideas

86. Recognizing and Comparing Kinetic Energy

91. Computing the Potential Energy

101. Solving More Complex Problems

4FF: Fundamental Forces & Fields (supplemental activities FF·1-29)

FF·1. Exploring Models of Electromagnetism

FF·5. Exploring the Magnetic Interaction

FF·9. Exploring the Gravitational Interaction

FF·11. Distinguishing Mass and Weight

FF·13. Using a Mathematical Model for the Electric Force

FF·20. Reasoning with Universal Gravitation

FF·25. Representing Vector Fields Using Field Line Diagrams

FF·27. Applying Work and Energy Ideas

4AT: Advanced Topics in Mechanics (supplemental activities AT·1-23)

AT·1. Exploring Ideas About Circular Motion

AT·5. Reasoning About Circular Motion

AT·9. Reasoning About Projectile Motion

AT·14. Reasoning About Relative Motion

AT·16. Graphing Rotational Motion

AT·17. Introducing Rotational Kinematics

AT·20. Solving Rotational Dynamics Problems

AT·21. Identifying Energy in Rotational Systems

4CS: Complex Systems

Nothing available here (yet??)...

Using MOP

An excerpt from the MOP teacher's guides about how to use MOP effectively

Introduction

This section describes how to get started with MOP. Ideally a teacher would work through all of the student activities and read through all of the accompanying materials in the MOP Teacher's Guides. Only then can a teacher make well-informed decisions about how to best use the MOP materials to meet their instructional needs and goals. Our experience, however, is that this ideal is unrealistic for most teachers. Teachers have little disposable time they can devote to mastering a new curriculum, and so, teachers must "learn as they go." It can take teachers as long as three years to become thoroughly comfortable and familiar with a new curriculum. We hope the contents of this section will help make getting started with MOP as efficient and effective as possible.

Getting Started covers the following areas:

To get the most out of this section, it is best to have your copy of the MOP materials handy and refer to it as needed. MOP Curriculum Materials

There are two sets of materials with MOP, a set of four booklets for students and a corresponding set of booklets for teachers. The first three booklets deal with topics in mechanics: Motion, Interactions, and Conservation Laws & Concept-Based Problem Solving. The fourth booklet --- Fields, Complex Systems & Other Advanced Topics --- applies the principles developed in the first three booklets to a wide range of physical phenomena.

Each student booklet is divided into two parts: The Activities form an integrated set of thoughtful engagements for students, and the Reader organizes and summarizes the ideas of the physics content and is meant to be read after students have engaged in associated activities.

Each corresponding Teacher's Guide also has two parts: Answers and Instructional Aids for Teachers, which provides advice for how to optimize the effectiveness of the activities, as well as brief explanations and comments on each question in the student activities, and Answer Sheets, which may be duplicated and distributed to students as desired. Use of the answer sheets is particularly recommended for activities requiring a lot of graphing or drawing.

The first booklet in the teacher series contains three supplements:

Components of a MOP Activity

The MOP activities all have the same basic structure:

Occasionally an activity will contain an additional component:

Although a MOP activity has several components, the Main Activity and Reflection are the most important. We recommend getting students to the Main Activity as quickly as possible and not overdoing the preparation of students. Students may struggle, but most of their difficulties can be addressed as they proceed through the activity. Students may feel frustrated initially, but with some reassurance from the teacher and a little experience facing and overcoming the inevitable confusion associated with starting something new, students will grow into confident and independent learners.

Nevertheless, it is worthwhile helping students become aware of the structure of the MOP activities. This can be done gradually and indirectly by meta-communicating with students. For example, on occasion ask students if they learned what they were expected to learn --- and how do they know. Sometimes have students consider whether they have the knowledge needed to do the upcoming activity. Test their knowledge by asking them some basic questions. Another good idea is to check whether students understood the directions given in the Main Activity. This can be accomplished by stopping the class (after students have had a reasonable chance to get started) and asking individual students or groups of students to share with the class how they are approaching the activity. Ask the class whether the approach meets all the requirements set forth in the directions. After students finish an activity ask students to tell you what is the purpose of the activity from their perspective.

About the MOP Reader

There is no traditional textbook with MOP. There is a Reader, but it serves mostly as a follow-up to the MOP activities. The intent is that students begin by working the activities with little or no preparation from the teacher or from any other source material. Any preparation that might be needed is provided in the Prior Experience / Knowledge Needed sections of the activities. The appropriate part of the Reader is designed to be read after the student finishes the corresponding activity (or set of activities), and is intended to summarize, organize and integrate the ideas and issues raised in the activities. The students can then use the Reader as a resource for later activities. Guidance for reading assignments is provided in the Instructional Aids. Contents of the Teacher Aids

The Answers and Instructional Aids for Teachers are our way of communicating the philosophy behind each activity and/or set of activities. We explain our goals and our expectations for each activity, and try to give warnings about student difficulties, misunderstandings, and common responses. We also suggest ways to interpret different patterns of students' responses as well as ways to assess student understanding. The Instructional Aids are intended to prepare teachers in their role as coaches of students' learning.

A Note on Laboratories, Demonstrations, and Hands-On Activities

The MOP approach stresses the value of building the physical representation for physics concepts and principles, and integrating this with more formal representations. Consequently, some of the activities involve extensive use of hands-on activities. Clearly, laboratory exercises and demonstrations also serve to develop the physical representation and a good course will employ these methods as well. We wish here to argue that simple, unstructured explorations of physical ideas in a qualitative, hands-on manner serves an important function not met by typical demonstrations and formal laboratories.

Traditional formal labs tend to be cook-book in nature, to involve large amounts of data manipulation and analysis, and frequently culminate in time-consuming lab reports. They are often unmotivated from the students' point of view and do not seem to impact learning of physics. To be sure, there are a multitude of skills to be learned from good laboratory experiences, but command of the physical representation is not a common result. Many excellent laboratory materials have already been published and we have elected not to duplicate that effort. In our experience most teachers have strong preferences for the laboratory exercises that they use and just about any laboratory is compatible with MOP.

In many classrooms, demonstrations are used to exemplify a particular concept or principle, with the interpretation, description and explanation provided by the teacher. For a thinking student, however, a demonstration often raises many more questions than it answers, and without the opportunity to investigate those questions, students can come away with very distorted views about what the demonstration means. To become convinced of this, ask your students what they think they have observed after a demonstration before you tell them what they should have observed. We recommend a broader use of demonstrations as a means for students to explore the features relevant for understanding physical systems and the reasoning used to analyze them. To maximize the effectiveness of demonstrations, we encourage teachers to use a reason-predict-show-explain sequence of activities, in which students think about the demonstration apparatus, predict what they believe will happen, observe the demonstration, and then describe the reasoning behind their predictions. (This is sometimes called an interactive demonstration.)

In our view, simple commonplace manipulatives, such as balls, marbles, springs, strings, and toy trucks, should be well integrated into the course. Students should have continuous access to these materials, and they should be frequently asked to employ them to demonstrate physical ideas and principles in a qualitative manner. This is a very difficult task for students. Perhaps the only thing more difficult for students than translating their ideas into physical reality is explaining what they are trying to accomplish to another person. For this reason small group or class discussions of hands-on activities are particularly fruitful for interrelating the linguistic, formal, and physical representations. Global Issues: Planning the School Year with MOP

How you implement MOP during your school year depends strongly upon your instructional objectives for your specific class. There are many possible objectives, ranging from preparing students for college science courses to exposing students to the broadest possible range of physics phenomena. Faced with a particular class, many teachers feel that these two objectives are in conflict and they must strike some compromise. Indeed, because time is limited, every teacher is constantly making choices regarding how to spend their class time.

We would argue that your most important objective is to make your students self-aware and self-motivated learners, and that MOP can help you accomplish this. Many students are intimidated by physics, feel inadequate to do physics and, consequently, disengage. Students spend far too much time looking for the right answer or, even worse, the answer they think you want. Discussing these issues and your expectations openly will help them focus on the only meaningful outcome, their own learning and development. Obviously, it is important to reward engagement and effort. Such rewards, however, should not confuse students by creating the impression that all reasoning is equivalent and just a matter of taste.

Touching upon many topics and modern phenomena is a desirable goal. Such exposure, however, is only effective and long lasting if students have some firm ground of fundamental concepts to which they can relate this knowledge. Building a solid foundation is what MOP is all about. Depending upon individual goals, the mechanics portion of MOP (i.e., the first three booklets) should occupy between 1/2 to 3/4 of the school year.

Although the MOP activities are numbered, there is no need to proceed through them in strict order. Nor is there a need to do every activity or any particular activity in its entirety. While there is no single best path through the materials, it is best not to invert related activities designed to target different cognitive stages. As mentioned in the Letter from the Authors and as elaborated in Supplement B: Concept-Based Problem Solving, MOP activities dealing with the same topic are sequenced in a cognitive sense. Students are encouraged to (a) explore their current understanding, (b) refine and interrelate their physics concepts, (c) enhance their analyzing and reasoning abilities, (d) develop problem-solving skills, and (e) organize their knowledge into a coherent structure.

Which activities should be used and how much time should be devoted to each of them is something only you can decide. The activities are intended to be a resource, not a recipe. We offer the following general advice for your consideration:

Creating a Lesson Plan Around a MOP Activity

Once you decide to use a MOP activity:

  1. If possible, invest the time to do the activity yourself. This is the best way to become familiar with the activity, and you will be in a better position to make decisions. Read over the instructional aids to get a general sense of the issues being addressed in the activity.
  2. Choose the hands-on materials that will be available.
  3. Decide how to introduce the activity. Should you let students just jump in, or should you ask a probing question beforehand, or should you do an interactive demonstration? For instance, you might discuss the Goals and Objectives with your class, or work on the example, or even do part of the activity as a class exercise.
  4. Select the portions of the activity you want to do, which parts will be done in class and which parts might be done for homework.
  5. Decide how students will engage in the activity. Should it be done as a class, in groups, in pairs, or individually? When should the class discussion begin? Should students present their answers to the rest of the class and, if so, how?
  6. Think about ways you can support students' progress through the activity.
  7. Select points for class discussion and/or question(s) to probe student understanding.
  8. Look at the explanations and comments provided with the answers to get some sense of how students might respond to the various questions and what these responses might mean.

Formative and Summative Assessment with MOP

Most assessments used by teachers are at the end of a topic and are of a summative nature, that is, they serve to evaluate student progress and assign a grade. Only rarely are tests designed to inform either students or teachers of the nature of student difficulties. Assessments of this second type are called formative because the results have consequences for subsequent instruction. Generally, it is preferred to identify student problems or misunderstandings while there is still time to do something to correct the situation. The MOP approach emphasizes the need for formative, as opposed to summative, assessment.

We know that the traditional ways of testing students do little to uncover conceptual difficulties or to measure knowledge of physical laws and principles. Traditional exam questions tend to stress answers and be numeric and formulaic in nature. New ways of assessing students' progress must necessarily be developed alongside new approaches to teaching. These new assessments need to encourage students to focus on those features that are important for deep understanding. Without new assessment methods, students will remain largely unwilling to abandon formulaic approaches. Examples of how new assessments might be structured to probe students' progress and their conceptual understanding can be found in the "Probing for Student Understanding" sections of the Answers and Instructional Aids for Teachers. Another suggestion is to reserve part of an activity for a later assessment. If students are to demonstrate their abilities, it is important that the assessment item resemble the tasks that they have rehearsed.

Finally, it is our view that tests and exams should serve primarily a pedagogic rather than evaluative function. Students dislike and resent exams because they feel evaluated, i.e. their worth is determined. Failure erodes their self-confidence and self-esteem. Success on traditional exams does not send a much better message. Successful students come to believe that achievement in the form of grades, rather than intellectual development, is the goal to be sought. Exams can be designed to be informative to students and can serve as valuable educational experiences for students. Students need to go beyond being active, or even engaged learners. They need to become self-invested in the entire process of education. They need to develop self-evaluation skills and good exams can help them achieve this goal. Frequently asking students to what they attribute their lack of success or inability to do a problem helps them establish self-reflection as the norm. Teaching self-invested and reflective students is an exciting and rewarding experience.

Where to Get MOP

Minds•On Physics is sold by the Kendall/Hunt Publishing Company.

For MOP Users

If you are a teacher using Minds*On Physics...

Are you a teacher who uses Minds•On Physics? If so, we'd love to hear from you. Please don't hesitate to contact Bill Leonard with any questions, comments, or feedback.

You should probably check out the MOP Errata page, too.

MOP Errata

Corrections for errors (gasp!) in the published MOP books

Believe it or not, we have errata lists for the following books. ("TG" means "Teacher's Guide" and "AR" means "Activities & Reader", i.e., the student activities book.) If you think you've found a mistake that we don't list here, please report it to Bill Leonard.

We'll add errata pages for the other books if/as the need arises.

Errata for Motion AR

Student Reader, p. R4, middle:

  • The components of the position of the ant should be given everywhere in "centimeters" not "meters". [EH, 06Jun04]

Student Reader, p. R9, top:

  • The average velocity from t = 5.0s to t = 6.0s is +10cm/s, not −10cm/s. [AW, 14Jan04]

Many thanks to Andrew Wertz of Littlestown HS in Littlestown, PA, and Ed Haley of E.C.O.S. in Springfield, MA, who found these mistakes.

Errata for Motion TG

Activity 4, p. 22, question P8, part (a) answer

  • Add graph D to the list of answers, i.e., "Graphs C, D, and E represent objects that are speeding up."

Activity 8, p. 39, "Link to Reader"

  • Change the ending page of the reading assignment to R9, i.e., "Students may read pages R8-9 (the beginning of section 1.4, Velocity) after finishing Activity 9."

Activity 9, p. 45, "Link to Reader"

  • Change the ending page of the reading assignment to R9, i.e., "Students may read pages R8-9 (the beginning of section 1.4, Velocity) after finishing this activity."

Activity 9, p. 46, "Probing for Student Understanding", question P3

  • In parts (a) and (c), change the units to cm/s, i.e., "P3. (a) Which object (in part A) reaches a velocity of 1cm/s first? (b) When does this occur? (c) Which object reaches a speed of 1cm/s first? (d) When does this occur?"

Activity 12, p. 65, question A4 answer, bullet 1

  • Change wording to "Students might plot speed vs. time instead of velocity vs. time (as shown below on the left). In addition, some students might not realize that the speed goes to zero between strobes 4 and 5 (as shown below on the right)."

Activity 12, p. 68, question B4 answer

  • Change answer to "after t = 0.45s".
  • Add third bullet, "• By exaggerating the curvature of the graph between #4 and #5, you can see that the marble is at the 1m mark just after the midpoint in time."

Activity 13, p. 76, question P1 answer

  • In part (a), at t = 1½s, object X is at x = 7½cm.

Activity 14, p. 79

  • question A2 answer, bullet 1, "Object J has the largest displacement..."
  • question A4 answer, bullet 1, "Students might pick only object J, because object I..."
  • question A4 answer, bullet 2, "Students might pick only object I..."
  • question A6 answer, "... which would correspond to J"
  • question A6 answer, bullet 1, "Students might pick object I because the curves for objects E and I look the same."

Activity 15, p. 86, question P1 answer

  • The answers to parts (a) and (b) are reversed.

Activity 16, p. 91, question C3 answer

  • Modify paragraph 2: "Yes, this answer agrees..."
  • Fix bullet 1: "Students might have gotten question B2 wrong."

Activity 17, p. 96, question A5 answer

  • Add to the end of paragraph 1, "At 20km/h, the plane travels about 5½km before losing contact with the car."
  • Add to the end of bullet 1, "i.e., after the plane has traveled 20km".

Activity 19, p. 107, question P4 answer

  • The speed is only 1 grid/s, i.e., the answer should read, "... the average velocity is +1 grid/s —or— 1 grid/s, to the right between 2s and 6s."

Activity 23, p. 131, question P8 answer

  • Add bullet, "• See table of values for P1 above."

Activity 24, p. 137, question B1 answer, bullet 4

  • Change A2-A4 to B2-B4, i.e., "Students do not need to make precise calculations to answer questions B2-B4."

Activity 25, p. 145, question A2 answer

  • In part (i), the Total Area (i.e., column 4) should be 292.5 m.

Activity 27, p. 163

  • question R2 answer is really only the first half of the answer to R2.

  • question R3 answer is really the second half of the answer to R2.

  • question R4 answer is really the answer to R3.

  • question R5 answer is really the answer to R4.

Many thanks to Lonnie Grimes of Oakmont High School in Roseville, CA, who found almost all of these mistakes.

Errata for Interactions AR

Activity 37, p. 146, "Explanation of Activity and Examples":

  • The page number indicating where to find the map (of King's Court) should be "143", not 134.

Many thanks to Patrick Diehl of Ashley Hall School in Charleston, SC, who found this mistake.

Errata for Interactions TG

Activity 36, p. 216, question A4 answer

  • Quadrant (column 1) should be "2 only", angle relative to horizontal (column 2) should be "27°", and angle relative to East axis (column 3) should be "153°".

Activity 36, p. 217

  • Answer to question B2 should be: 580m @ 149°.
  • Answer to question B3 should be: 500m @ 307°.
  • Answer to question B3, bullet 1: replace -37° with -53°.

Activity 37, p.222, "Suggested Points for Class Discussion", bullet 2

  • The word 'needs' should be 'need', i.e., "... both the origin and the orientation of the coordinate frame need to be specified..."

Activity 38, p. 227, question A5 answer

  • All the answers for vector V are wrong. There should be a minus sign in front of each term, and the length of the vector is 4.24cm. So, the x-component of V can be written either -(4.24cm) cos(45°) or -(4.24cm) sin(45°), and the y-component of V can be written either -(4.24cm) sin(45°) or -(4.24cm) cos(45°).

Activity 38, p. 229, question B5 answer, bullet 2

  • Change B3 to B2, i.e., "Students might use a rotated coordinate system (as in B2)."

Activity 42, p. 258, question B1 answer, bullet 1

  • Rephrase third sentence to read, "This is the only situation in this part for which buoyancy is considered relevant."

Activity 44, p. 267, "Probing for Student Understanding"

  • Change part (b) of question P3 to read, "In part B, how would the readings on scales A, B, and D change if scale C were removed?"

Activity 45, p. 280

  • In the answer to question I7, add object E to the list, i.e., "Only objects A, B, D, and E must have friction forces exerted on them."
  • The answer to question R3 is missing. It should read, "The objects considered in situations A3, A6, and B3 could be accelerating. For the rest, the object has a constant velocity.
  • There are no comments for R3. They are,
  • "Students might not include A3, perhaps because they think the ball is not accelerating at the top of its trajectory."
  • "Students might include B1, perhaps because the book is accelerating. But the object being considered is the table, which is not accelerating."
  • "Students might not include B3, perhaps because they think that the ball is at rest when it is touching the wall."
  • "At this point in the course, students are not expected to know the relationship between force and acceleration. Students should be encouraged to determine which objects definitely have no acceleration. The rest can be considered to possibly be accelerating."
  • The answer for question R4 is missing. It should read, "(Students indicate any forces other than the seven introduced here that they have heard of. They then indicate if any of these other forces behave like any of the forces introduced here."

Activity 45, p. 281

  • The answer to question P5 is wrong. It should read, "If the spring was compressed rather than stretched, then the strings would be angled inward, rather than outward. In other words, object G would be hanging to the left of where its string is attached to C, and object H would be hanging to the right of where its string is attached to C."
  • The comment for the answer to question P5 does not fit any longer. It should read, "Students might not think it is possible for the spring to remain compressed between objects G and H."

Activity 46, p. 284, "(More Ways of) Probing for Student Understanding"

  • Question P6 is question P4.
  • Question P7 is question P5.
  • Question P8 is question P6.

Activity 47, p. 294, question R2 answer

  • Change 'part B' to 'part A', i.e., "In situation C of part A, the normal force..."

Activity 48, p. 297, "Suggested Points for Class Discussion", bullet 2, last sentence

  • The word 'a' should be 'at', i.e., "(Thus, one can be at rest; the friction is still kinetic.)"

Activity 49, p. 307

  • The first entry in the table is not the beginning of the answer to question A4, but a continuation of the answer to question A3.
  • The answer to question A4 begins with gravitation.
  • There is a force missing from the answer to question A4. The force (i.e., column 1) is "kinetic friction." The way it will be determined (column 2) is "Multiply the normal force by the coefficient of kinetic friction. Direction is opposite the motion of _m_1." The magnitude & direction (column 3) is "(NA)." Comment is "• We do not actually know the normal force, so we cannot determine the force of kinetic friction. However, students might think that they know the normal force using common sense."

Activity 49, p. 308, question R1 answer

  • The second bullet for air resistance is wrong. It should read, "At very small speeds, the force law is closer to Bv.

Activity 51, p. 324

  • The answer to question B1, part (a) is wrong. The x-component of F_N_,left should be F__N,left.
  • The answer to question B1, part (b) is wrong. The x-component of F_N_,right should be -F__N,right.
  • The answer to question B2, part (c) is confusing. Vectors F_g_1, F_N_2, and F_T_2 are not part of the answer. They are simply the other vectors in the situation, which are included because their components are known.
  • The answer to question B2, part (d) is wrong. The x-component of F_g_2 should be -F__g_2 cos 60°, and its _y-component should be -_F__g_2 sin 60°.
  • The word "the" should be removed from the second line of the last bullet for the answer to question B2, i.e., "Even if we notate the magnitude of both tension forces as..."

Activity 54, p. 350, question P9 answer

  • Change "velocity" to "velocities", i.e., "(a,b) The forces... Kinetic Friction, which depends on the relative velocities of the objects in contact, and..."

Activity 55, p. 357, question A5 answer

  • In the table showing the time intervals during which the ball is accelerating, change '4.9s' to '4.8s', i.e., the time interval corresponding to the 2nd time the ball is rolling across the felt should be [4.8s, 6.5s].
  • In the table showing time intervals during which its velocity is constant (it's part of the 4th bullet of the answer to question A5), change '4.9s' to '4.8s', i.e., the third time interval during which the ball is rolling at constant velocity is [3.51s, 4.8s].

Activity 56, p. 370, question C4 answer, bullet 3

  • Change 'any' to 'a', i.e., "Students might not perceive that there is a net force on them when they walk in a circle."

Activity 58, p. 384, question A2, part (c) answer

  • Of the three free-body diagrams, the one on the left is for the skydiver, the one in the middle is for the parachute, and the one on the right is for the Earth.

Activity 58, p. 386, question B4 answer

  • Add to the end of the answer to part (b): "But perhaps not as much faster and farther as before, assuming for example that she does not push as hard as her father did before."
  • Add a bullet: "• In other words, her speed might be smaller than it was before, but it is always larger than her father's."

Activity 58, p. 387, question R1 answer, bullet 1

  • Change to "The action-reaction pair has five features: exerted by different objects, exerted on different objects, same type (normal, gravitational, etc.), same magnitude, and opposite direction."

Activity 59, p. 389, "Suggestions for Classroom Use"

  • Change bullet 2 to: "Focus students' attention on learning the answers and explanations to two questions using the following group structure: Divide the class into teams of 3 or 4 students each. Assign each team 2 questions from the same part, or put slips of paper with the numbers of 2 questions into a bowl and have teams choose. Tell students that each of them will be asked to write out the explanation to one of the questions, and that each student's grade will depend in part on how well the other team members do. As the teams are working, decide which explanation each student will provide. When the working time is complete, give students their assignments, to be done either during or after class. When grading explanations, give half credit for each individual's contribution and half credit for the contributions of the rest of the team. In other words, half of each student's grade will depend on his/her individual explanation, and the other half will depend on his/her team's explanations.
  • Insert between bullets 2 and 3: "• For small classes with only a few teams, do parts B and D first, then repeat with parts C and E."
  • Add bullet: "• As a class, compare answers and discuss areas of disagreement."

Activity 59, p. 391, question A4 answer

  • Change 'rope 1' to 'rope 2', i.e., "... then the tension in rope 2 is larger in case II than in case I."

Activity 59, p. 392, question C2 answer

  • Add bullet: "• Students might think that the velocity is larger because the net force is larger."

Activity 60, p. 402, question R2, part (a) answer

  • Remove 'of the', i.e., "The mass is much larger for the car."

Many thanks to Lonnie Grimes of Oakmont High School in Roseville, CA, who found almost all of these mistakes.

Errata for Conservation Laws TG

Activity 74, p. 513, question B3, part (c) answer

  • In the second paragraph, the area of each 'box' is wrong. It should be 0.01N-s, i.e., "... and each box has an area of (2N) x (0.005s) = 0.01N-s..."

Activity 76, p. 529, question A3 answer

  • The parts are not labeled, i.e., the "(a)", "(b)", and "(c)" labels are missing.

Activity 76, p. 532

  • The answers and comments to questions R1, R2, and R3 are missing.
  • The answer for R1 is, "Total momentum is conserved for situations A3 and A6. It is zero initially, and remains the same throughout the time interval specified. Total momentum is approximately conserved for situation A1, because the impulse delivered to the system by gravitation is small during the explosion. At least one component of the total momentum is conserved for the other 5 situations. We define the x-direction to be the horizontal in the plane of the page (i.e., to the right), the y-direction to be the vertical, and the z-direction to be the horizontal perpendicular to the plane of the page (i.e., directly toward you). In situations A2, A4, and A7, the net external force is in the y-direction, so total momentum is conserved in the x- and z-directions. In situation A5, the net external force has y- and z-components, so momentum is conserved only in the x-direction."
  • The comments for R1 are:
    • Students might think that momentum is not conserved in situation A6, because the wheel is slowing down.
    • Students might consider only the ball in A3, rather than the Earth-ball system.
    • In situation A3, students might not ignore the gravitational forces exerted on the Earth-ball system by the Sun, the Moon, and the planets.
    • Students might not recognize that the total momentum of the Earth-ball system is staying the same during the motion of the ball.
    • Students might only consider two directions, i.e., the x- and y-directions.
    • In situation A5, we are assuming that the bow string exerts a force on the arrow in the yz-plane.
    • Students might think that momentum is not conserved in any direction in situation A7, because the ball's are going in all directions.
  • The answer for R2 is, "In situations A3 and A6, all forces are internal; the net force on each system is zero."
  • The comments for R2 are:
    • If students do not have the correct set of situations here, they are likely to generalize improperly.
    • Students might not realize that in A3 they are expected to ignore the forces exerted by the Sun, the Moon, and the other planets.
    • Students might not realize that in A6 the net force on the wheel is zero, because it is slowing down.
  • The answer to R3 is, "For those situations in which momentum is not conserved, there are external forces on the specified system. In each case, the direction of the change in momentum is the same as the direction of the net external force. In order to always conserve momentum, it is necessary to choose a system large enough so that there are no external forces on it. If we include the Earth in each system and ignore the gravitational forces exerted by the Sun, the Moon, and the planets, then momentum is conserved in all the situations."
  • (There are no comments for R3 at this time.)

Activity 83, p. 584, question A1 answer

  • The explanation (column 5) should read, "Monkey exerts F__N_1 and _Ffs. Whatever is holding up the rope exerts _F__N_2 (assuming, e.g., that the rope is tied to a hook in the ceiling). The displacement of the rope is zero."

Activity 87, p. 616, "Anticipated Difficulties for Students", bullet 7 (i.e., last bullet)

  • The 'clay' should be a 'cart', i.e., "Analyzing the cart in situation R3... because the work done on the cart is done..."

Activity 87, p. 618, "Providing Support to Ensure Student Progress", bullet 6 (i.e., next to last bullet)

  • Change to: "In situation R3, focus students attention on forces that are applied through a displacement, such as forces internal to the spring, rather than forces that are applied through zero displacement, such as the normal force exerted by the wall."

Activity 87, p. 620, question A3(b) answer

  • The explanation is wrong, because we do not know how to calculate the work done by friction, as described in the Reader. Therefore, students are expected simply to use common sense to try to answer this question. Later, the explanation will be that there is a loss of energy from the macroscopic realm to the microscopic realm, which means that the speed must be smaller after hitting the spring than before.

Activity 87, p. 620, question A3(b) bullet

  • The comment is inappropriate for the same reason that the explanation is inappropriate, that is we do not know how to calculate the work done by friction, as described in the Reader. It should read, "The work done by the friction force on the cart cannot be calculated or even estimated. Further, knowing its value would be of no consequence here, because all of the macroscopic kinetic energy lost by the cart becomes microscopic energy of the cart. In other words, the forces are internal to the cart, so the energy remains with the cart. However, at this point in the course, students are not expected to be able to make this distinction between macroscopic and microscopic energy."

Many thanks to Lonnie Grimes of Oakmont High School in Roseville, CA, who found almost all of these mistakes.

Errata for Advanced Topics AR

The following mistakes are in the first 3 printings of Vol. 4·AT / Activities & Reader. If you have a 4th printing or higher, they have been fixed. Please check the copyright page (page iv) to see which printing, or mixture of printings, you have.

Contents, p. v

  • The correct title of Activity AT·13 is "Exploring Relative Motion in One and Two Dimensions".

Activity AT·4, p. 13, "Prior Experience/Knowledge Needed"

  • The label of the first equation should read: tangential component of acceleration. The change in speed can be negative, and when it is, the direction of the tangential component of acceleration is opposite the direction of motion. And when the change of speed is positive, this component is in the direction of motion.

Activity AT·8, p. 30, question A3

  • In the description of the situation, the speed of the marble three seconds later should be "80cm/s", not "79cm/s".

Activity AT·8, p. 31, question B2

  • In the description of the situation, the second sentence should begin: "One second later..."

Activity AT·8, p. 31, question B3

  • In the description of the situation, the time at which the toy car stops near the top of the incline should be "t = 0.58s", not "t = 1.8s".
  • The fourth question in part (d) should be: What is the car's position and velocity at "t = 0.68s", not "t = 2s".

Activity AT·11, p. 44, question A1

  • In the description of the situation, the initial speed of the puck should be "250cm/s", not "25cm/s".

Activity AT·17, p. 69, questions B1 & B2

  • A car traveling at 29m/s is moving at "65mi/h", not "60mi/h". This mistake occurs twice in question B1 and once in question B2.

Activity AT·17, p. 69, question B3

  • The diagram of situation A is not consistent with what is happening. In particular, there is not enough string left hanging to allow the wheel to spin as many times as it needs before stopping. The following diagram replaces the one accompanying the description. Right-click or command-click and choose “Open image in new window” (or equivalent) to see a full-sized version. Print that version at 100% for a transparency, or at 33% to replace the figure in students’ books. Also note that the diagram on the answer sheet is the Teacher's Guide is the same as that shown below. Finally, the angle of the incline in situation B has been made more shallow to be consistent with the additional changes listed below.
  • Many of the values for the given information should be changed. The initial speed of the wheel is now 1rev/s, and it is slowing down at a rate of ¼rev/s2. The ball is now a marble, and it is rolling up the incline at 4m/s and slowing down at a rate of 1m/s2. (Changes shown in bold type.)
  • The question for part (b) should read: "Write an expression for the position of the marble..." (Change shown in bold type.)

Activity AT·18, p. 73, question A5

  • In part (b), when the car speeds up, its speed in miles per hour should be "65mi/h", not "60mi/h". In other words, 29m/s = 65mi/h.

Activity AT·21, p. 86, question R4

  • The "second" part (b) should be part (c).
  • Part (c) should be part (d).

Errata for Complex Systems AR

The following mistakes are in the first printing of Vol. 4•CS / Activities & Reader. If you have a 2nd printing or higher, they have been fixed. Please check the copyright page (page iv) to see which printing, or mixture of printings, you have.

Activity CS•3, p. 13, question A2(c)

  • The mass of oil (fluid X) should be "16" (grams), not "18".

Activity CS•11, p. 50, property #4 of idealized fluids (at the very bottom of the page)

  • The middle of the sentence should read: "... which means that both the pressure and speed are constant...".

Activity CS•11, p. 51, "Explanation of Activity"

  • The mass of 10cm3 of oil should be "8g", not "9g".

Activity CS•11, p. 51, figure for problem A3

  • The following figure should make it clearer to students what is going on here, i.e., the direction in which the glass tube is rotated so that it "rests on its side" in part (a). Right-click or command-click and choose "Open image in new window" (or equivalent) to see a full-sized version. Print that version at 100% for a transparency, or at 33% to replace the figure in students' books. (The answer sheet in the Complex Systems TG already has the corrected figure.)

Activity CS•12, p. 53, "Purpose and Expected Outcome"

  • The last sentence should begin: "When you find a system to which you cannot apply..." (Change shown in bold type.)

Activity CS•22, p. 106, question A2

  • Part (a) should read: "Which state(s) has the highest temperature? Explain."
  • Part (b) should read: "Which state(s) has the lowest temperature? Explain." (Changes shown in bold type.)

Activity CS•26, p. 127, description for part B

  • The springs being studied in this part of the activity are said to be "relaxed". This word should be omitted. Instead, the springs should be considered to have zero or very small relaxed length. The need for this change is that when the springs are relaxed initially, the balls attached to them in situation B1 would tend to move left and right as well as up and down, which is unnecessarily complicated. By making the relaxed length very small, the motion of the balls (in B1) becomes purely transverse, i.e., up and down. Note that this change affects only the results of B1.

Activity CS•30, p. 151, questions D3 and D4

  • The question in D3 should read: "Will the wave form on the lighter spring move faster or slower than the original wave form on the heavier spring?"
  • The question in D4 should begin: "Will the wave form on the lighter spring..." (Changes shown in bold type.)

Reader/Chapter 1: Fluids, p. R18, table showing speeds of water outside holes

  • The list of speeds in the last column are wrong. The correct table is shown below. (Right-click or command-click and choose "Open image in new window" or equivalent to see a full-sized version, then print at 50% to replace in student books.)

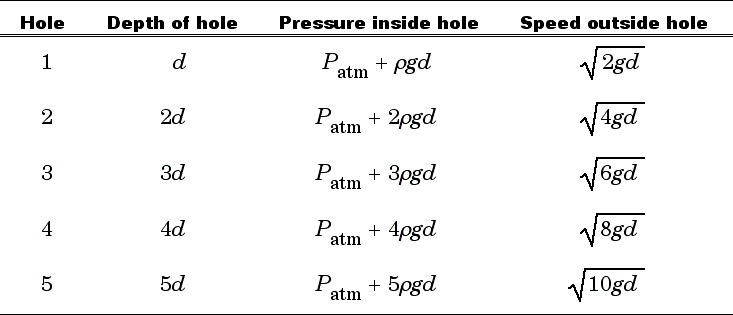
Reader/Chapter 1: Fluids, p. R19, table showing speeds of water outside holes and where the water lands

  • The list of speeds in the third column and the list of where the water lands in the last column are wrong. The correct table is shown below. (Right-click or command-click and choose "Open image in new window" or equivalent to see a full-sized version, then print at 50% to replace in student books.)

Many thanks to Prof. Josip Slisko of the Faculty of Physical and Mathematical Sciences at the Benemerita Public University in Puebla, Mexico, who found many of these mistakes.